Tree Search
结点定义
1 | // 二叉树 |
层序遍历
- 二叉树的层序遍历
1 | // 迭代 |
- 多叉树的层序遍历
1 | vector<vector<int>> level_order(Node* root) { |
二叉树先序/中序/后序/Morris
先序遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22// 递归
void travel(Node *root, vector<int>& vec) {
if (!root) return;
vec.push_back(root->val);
travel(root->left, vec);
travel(root->right, vec);
}
// 迭代
vector<int> preorder(Node *root) {
if (!root) return {};
vector<int> ans;
stack<Node*> s;
s.push(root);
while (!s.empty()) {
Node *cur = s.top(); s.pop();
ans.emplace_back(cur->val);
if (cur->right) s.push(cur->right);
if (cur->left) s.push(cur->left);
}
return ans;
}中序遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24// 递归
void travel(Node *root, vector<int>& vec) {
if (!root) return;
travel(root->left, vec);
vec.push_back(root->val);
travel(root->right, vec);
}
// 迭代
vector<int> travel(Node *root) {
vector<int> ans;
stack<Node *> s;
Node *cur = root;
while (cur || !s.empty()) {
while (cur) {
s.push(cur);
cur = cur->left;
}
cur = s.top(); s.pop();
ans.push_back(cur->val);
cur = cur->right;
}
return ans;
}后序遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46// 递归
void travel(Node *root, vector<int>& vec) {
if (!root) return;
travel(root->left, vec);
travel(root->right, vec);
vec.push_back(root->val);
}
// 迭代1
vector<int> travel(Node *root) {
vector<int> ans;
stack<Node *> s;
Node *cur = root;
Node *last_vis = nullptr;
while (cur && last_vis != root) {
while (cur && cur != last_vis) {
s.push(cur);
cur = cur->left;
}
cur = s.top(); s.pop();
if (cur->right == nullptr || cur->right == last_vis) {
ans.push_back(cur->val);
last_vis = cur;
} else {
s.push(cur);
cur = cur->right;
}
}
return ans;
}
// 迭代2
vector<int> postorderTraversal(TreeNode* root) {
if (!root) return {};
stack<TreeNode*> s;
deque<int> res;
s.push(root);
while (!s.empty()) {
TreeNode *cur = s.top(); s.pop();
res.push_front(cur->val);
if (cur->left) s.push(cur->left);
if (cur->right) s.push(cur->right);
}
return vector<int>(res.begin(), res.end());
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73void morris(TreeNode* root) {
if (!root) return;
TreeNode* cur = root, *mostRight = nullptr;
while (cur) {
mostRight = cur->left;
if (mostRight) {
while (mostRight->right && mostRight->right != cur) {
mostRight = mostRight->right;
}
// mostRight是cur左子树最右结点
if (mostRight->right) { // 第一次来到cur
mostRight->right = cur;
cur = cur->left;
continue;
} else { // mostRight->right == cur
mostRight->right = nullptr;
}
}
cur = cur->right;
}
}
void morrisPreorder(TreeNode* root) {
if (!root) return;
TreeNode* cur = root, *mostRight = nullptr;
while (cur) {
mostRight = cur->left;
if (mostRight) {
while (mostRight->right && mostRight->right != cur) {
mostRight = mostRight->right;
}
// mostRight是cur左子树最右结点
if (mostRight->right) { // 第一次来到cur
cout << cur->val << " ";
mostRight->right = cur;
cur = cur->left;
continue;
} else { // mostRight->right == cur
mostRight->right = nullptr;
}
} else {
cout << cur->val << " ";
}
cur = cur->right;
}
}
void morrisInorder(TreeNode* root) {
if (!root) return;
TreeNode* cur = root, *mostRight = nullptr;
while (cur) {
mostRight = cur->left;
if (mostRight) {
while (mostRight->right && mostRight->right != cur) {
mostRight = mostRight->right;
}
// mostRight是cur左子树最右结点
if (mostRight->right) { // 第一次来到cur
mostRight->right = cur;
cur = cur->left;
continue;
} else { // mostRight->right == cur
mostRight->right = nullptr;
}
}
cout << cur->val << " ";
cur = cur->right;
}
}
void morrisPostorder(TreeNode* root) {
}
多叉树先根/后根
- 先根遍历
1 | // 递归 |
- 后根遍历
1 | // 递归 |
Graph Search
笔试一般化为平时擅长的图表示再去做算法。
图的表示及转换
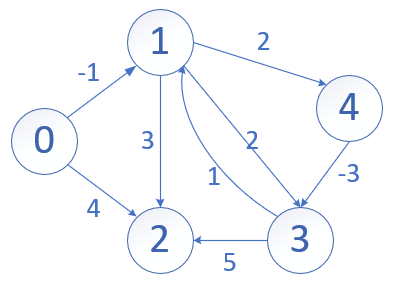
- 邻接矩阵
| i/j | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | 0 | -1 | 4 | \(\infty\) | \(\infty\) |
| 1 | \(\infty\) | 0 | 3 | 2 | 2 |
| 2 | \(\infty\) | \(\infty\) | 0 | \(\infty\) | \(\infty\) |
| 3 | \(\infty\) | 1 | 5 | 0 | \(\infty\) |
| 4 | \(\infty\) | \(\infty\) | \(\infty\) | -3 | 0 |
用vector<vector<int>> g(n, vector<int>(n, INF))表示，g[i][j]表示从顶点\(i\)到顶点\(j\)的权重，空间复杂度\(O(|V|^2)\)，适用于稠密图，用的不多；
- 邻接表：链表比较少用，基本都用动态数组。
| 0 | (1,-1) | (2,4) | - | - | - |
|---|---|---|---|---|---|
| 1 | (2,3) | (3,2) | (4,2) | - | - |
| 2 | - | - | - | - | - |
| 3 | (1,1) | (2,5) | - | - | - |
| 4 | (3,-3) | - | - | - | - |
用vector<vector<pair<int, int>>> g表示，g[i][j].first表示从顶点\(i\)出发到达的顶点\(k\)，g[i][j].second表示从顶点\(i\)到顶点\(k\)的权值，空间复杂度\(O(|V|+|E|)\)。 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26// 邻接矩阵转邻接表
vector<vector<pair<int, int>>> to_adj_list(vector<vector<int>>& adj_matrix) {
int n = adj_matrix.size();
vector<vector<pair<int, int>>> ans(n);
for (int i = 0; i < n; ++i) {
vector<pair<int, int>> tmp;
for (int j = 0; j < n; ++j) {
if (adj_matrix[i][j] != INT_MAX)
tmp.emplace_back(make_pair(j, adj_matrix[i][j]));
}
ans[i] = tmp;
}
return ans;
}
// 邻接表转邻接矩阵
vector<vector<int>> to_adj_matrix(vector<vector<pair<int, int>>>& adj_list) {
int n = adj_list.size();
vector<vector<int>> ans(n, vector<int>(n, INT_MAX));
for (int i = 0; i < n; ++i) {
for (pair<int, int>& p : adj_list[i]) {
ans[i][p.first] = p.second;
}
}
return ans;
}
边表
每个三元组表示一条边，上图的所有边表示为：\((0,1,-1),(0,2,4),(1,2,3),(1,3,2),(1,4,2),(3,1,1),(3,2,5),(4,3,-3)\) 用vector<vector<int>> e表示，e[i][0]表示顶点\(u\)，e[i][1]表示顶点\(v\)，e[i][2]表示\(u\)到\(v\)的权值，空间复杂度\(O(|E|)\)。链式前向星
空间复杂度\(O(n)\)，结合了邻接表和边表，包括边表数组edge和头结点数组head，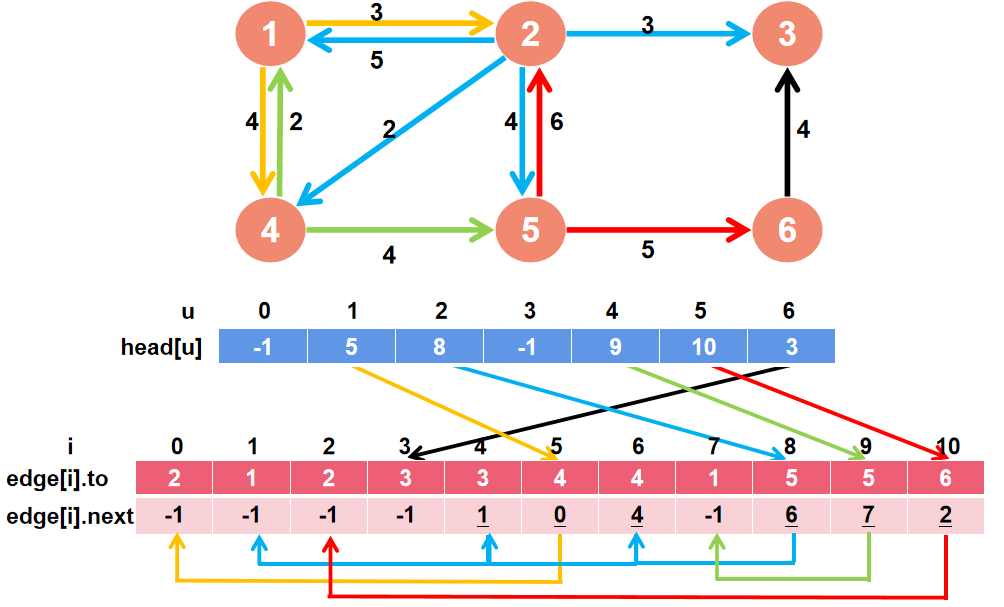
从结点2出发的边有4条，第一条边head[2]=8意味着该边存在edge[8]，下一条边存在edge[6]，next==-1表示结束。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26struct edge {
int to, next, w; // 边终点to 下一条边next 权值w
} edge[1000000];
int head[1000000]; // head[i]表示指向i的第一条边的存储位置
int cnt; // 记录edge的末尾位置
void init() {
for (int i = 0; i < 1000000; ++i) {
edge[i].next = -1;
head[i] = -1;
}
cnt = 0;
}
void addEdge(int u, int v, int w) {
edge[cnt].to = v;
edge[cnt].w = w;
edge[cnt].next = head[u];
head[u] = cnt++;
}
// 遍历结点i的所有邻接点
for (int i = head[u]; i != -1; i = edge[i].next) {
}
BFS
1 | def bfs(g, s): |
双向BFS 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36int dbfs(int s, int e) {
if (s == e) {
return 0;
}
queue<int> q1, q2;
q1.push(s), q2.push(e);
unordered_set<int> vis1{s}, vis2{e};
int res = 0;
while (!q1.empty() && !q2.empty()) {
if (q1.size() < q2.size()) {
int size = q1.size();
while (size--) {
int cur = q1.front(); q1.pop();
for (int nei : cur.neighbors) {
if (vis1.count(nei)) continue;
if (vis2.count(nei)) return res;
vis1.insert(nei);
q1.push(nei);
}
}
} else {
int size = q2.size();
while (size--) {
int cur = q2.front(); q2.pop();
for (int nei : cur.neighbors) {
if (vis2.count(nei)) continue;
if (vis1.count(nei)) return res;
vis2.insert(nei);
q2.push(nei);
}
}
}
++res;
}
return -1;
}
DFS
从起点出发，标记走过的点，如果发现没有走过的点，随便选一个向前走，无路可走就回退。
1 | def dfs(g, s): |
很不幸的是：上面的代码是错的。举个例子：g有ABCDEF6个结点，边为AB AC BC BD CD CE DE DF，如果走ABDE的话，最终答案应该是ABDECF，但是上述代码的结果是ABDEFC，显然不是合法的DFS结果。
问题在于标记结点是否访问的时机不对，在D弹出后，直接把EF入栈并标记为已访问，下次到E时发现C已被标记，但此时C很明显并未访问。
不应在入栈时标记，而应该在弹出时标记。因为入栈时并没有真正地访问该节点，出栈时才真正访问。
可以参考CS61B，正确的代码如下，可能会导致重复入栈（有方法避免）：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22def dfs(g, s):
stack = []
marked = set()
stack.append(s)
while (len(stack) > 0):
cur = stack.pop()
if cur not in marked:
marked.add(cur)
print(cur)
for adj in g[cur]:
if adj not in marked:
stack.append(adj)
def dfs(g, s):
global marked
marked = set()
marked.add(s)
print(s)
for adj in g[s]:
if adj not in marked:
dfs(g, adj)
判断从V出发能否走到终点
1
2
3
4
5
6
7
8
9bool dfs(v) {
if (v is terminal) return true;
if (vis[v]) return false;
vis[v] = true;
for (u in adj(v)) {
if (dfs(u)) return true;
}
return false;
}判断从V出发能否走到终点，若能，记录路径
栈的作用就是在走投无路之时留给你的退路。
1 | Node path[MAX_LEN]; // MAX_LEN取节点总数即可 |
- 遍历图上所有节点
邻接矩阵存储遍历复杂度\(O(n^2)\)，因为对每个节点，都要判断其它所有节点是否相邻。 邻接表遍历复杂度\(O(n+e)\)。
1、城堡问题 给一个地图以及每个格子周围的墙所代表数字之和，求该地图有多少房间，最大房间的面积。
分析：
要先判断每个格子周围有什么墙，注意到1，2，4，8的二进制形式0001、0010、0100、1000，所以只要将输入数字与1，2，4，8相与，就能知道该方块周围有什么墙。
把方块看作节点，相邻两个方块如果没有墙，就在这两节点之间连一条边，转换为图。
房间个数：图中的极大连通子图个数
极大连通子图：一个连通子图，加任意一个图中的其他点就不连通，这个子图就是极大连通子图。
具体： 对每个房间进行DFS，得到该房间所在的极大连通子图，染色所有能够到达的房间，最后统计共用了几种颜色以及每种颜色的数量。
1 |
|
2、踩方格 递归，从\((i,j)\)出发走n步的方案数就等于先走一步，从其它三个格子走n-1步的方案数之和。 前提就是该方块没走过。
1 |
|
3、ROADS
很多时候，并不需要一条路走到黑，这就是深搜中的剪枝。
1 |
|
