SVM是入门机器学习绕不开的一个话题,但愿这篇文章我能把它讲清楚。
线性可分
SVM的核心思想是:对于\(p\)维输入数据集,找一个有着maximum
margin的\(p-1\)维的超平面去做decision
boundary,这与直觉是相符的:
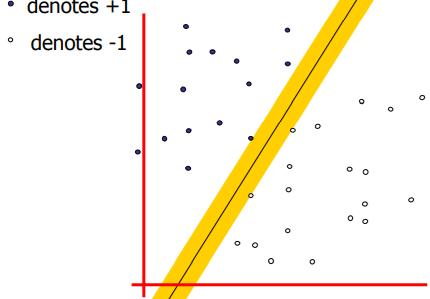
回忆下小学数学讲过的几何知识:空间中一个超平面由法向量\(\vec w\)和截距\(b\)唯一确定: \[a(x-x_1)+b(y-y_1)+c(z-z_1)+...=0, \\
w^Tx+b=0\] 那么如何求解最优超平面的\(w\)和\(b\)呢?
假设\(\vec w\)指向的一侧为正类(设为负类也没关系,后面会统一表示的),还假设在正类的支持向量上有\(w^Tx+b=1\),在负类的支持向量上有\(w^Tx+b=-1\),这里之所以将间隔假设为1主要是为了方便表示和求解,并不影响最终求得的最优超平面和决策函数,证明如下:
假设正类支持向量距最优超平面距离为\(c(c>0)\),即\(w^Tx+b=c\),此时对应的最优超平面为\(w^Tx+b=0\);又\(\frac{w^T}{c}x+\frac{b}{c}=1\),即\(w\)和\(b\)同时缩小\(c\)倍,那么这时超平面方程同除以\(c\)并不改变其形式。
因此对于正负样本有: \[w\cdot x_++b\geq 1 \\ w\cdot x_-+b\leq -1 \] 为了统一表示上面2种情况,引入\(y_i=\begin{cases} 1,&\text{+sample}\\ -1,&\text{-sample} \end{cases}\),所有样本统一表示为: \[y_i(w\cdot x_i+b)-1\geq 0\] 如果能确定\(b\)和\(w\),那么分类超平面和决策函数也就随即确定。
根据小学数学,间隔即为2个平行超平面的距离: \[width=\frac{(b+1)-(b-1)}{||w||}=\frac{2}{||w||}\tag{1}\]
综上,原优化问题为: \[ \begin{array}{ll} \min _{w, b} & \frac{1}{2}\|w\|^{2} \\ \text { s.t. } & y_{i}\left(w \cdot x_{i}+b\right)-1 \geqslant 0, \quad i=1,2, \cdots, N \end{array}\tag{2} \] 这里之所以构造为\(\frac{1}{2}\|w\|^{2}\)而不是\(||w||\)是为了后面构造的Lagrangian求导的便利。
明眼人都看得出来:优化目标是一个Convex Quadratic Optimization Problem,并且只有线性约束条件,意味着不会卡在局部极大,一定可以找到全局最优解。此时上述问题已经完全可以用一些QP软件求解了。之所以还要继续讨论下去得到其对偶形式,一是为了在高维空间应用kernel,二是对偶形式的求解有着更加高效的算法。
回忆下学过的高等数学:有约束优化问题可以通过拉格朗日乘子法求解。首先构造Lagrangian:
\[L(w,b,\alpha)=\frac{||w||^2}{2}-\sum_{i=1}^{N}\alpha_i[y_i(w\cdot
x_i+b)-1],\alpha_i\geq0\tag{3}\] 如果\(w\)和\(b\)满足\((2)\)中的约束,那么\(\max_{\alpha}L(w,b,\alpha)=\frac{||w||^2}{2}\);
如果\(w\)和\(b\)不满足\((2)\)中的约束,那么\(\max_{\alpha}L(w,b,\alpha)=+\infin\)。
因此下式的优化问题与\((2)\)完全等价:
\[
\min_{w, b}\max_{\alpha} L(w, b, \alpha)\tag{4}
\] 根据拉格朗日对偶性(不懂就暂时当作成立吧嘻嘻),\((4)\)的对偶问题为: \[
\max_{\alpha} \min_{w, b} L(w, b, \alpha)\tag{5}
\] 为了求解对偶问题\((4)\),先求\(L\)对\(w,b\)的极小,再求对\(\alpha\)的极大:
- 固定\(\alpha\),求\(\min_{w, b} L(w, b, \alpha)\) 分别求\(L\)对\(\vec{w}\)和\(b\)的偏导并令其为0: \[\frac{\partial L}{\partial\vec{w}}=\vec{w}-\Sigma\alpha_iy_ix_i=0, \vec{w}=\Sigma\alpha_iy_ix_i \\ \frac{\partial L}{\partial b}=\Sigma\alpha_iy_i=0, \Sigma\alpha_iy_i=0\tag{6}\] 决策向量\(\vec{w}\)是样本的线性和,将\(\vec{w}\)代入\((3)\): \[\min_{w, b}L=\Sigma\alpha_i-\frac{1}{2}\Sigma_i\Sigma_j\alpha_i\alpha_jy_iy_jx_i\cdot x_j\tag{7}\]
- 求\(\min_{w, b} L(w, b, \alpha)\)对\(\alpha\)的极大 即求\((7)\)对\(\alpha\)的极大,等价于取负号求对\(\alpha\)的极小,于是终于得到了原优化问题\((2)\)的对偶优化问题: \[ \begin{array}{ll} \min _{\alpha} & \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)-\sum_{i=1}^{N} \alpha_{i} \\ \text { s.t. } & \sum_{i=1}^{N} \alpha_{i} y_{i}=0 \\ & \alpha_{i} \geqslant 0, \quad i=1,2, \cdots, N \end{array}\tag{8} \]
利用SMO等算法可以比普通的二次规划算法更高效求得最优的\(\alpha^*\),进而根据\((6)\)求得: \[w^{*}=\sum_{i=1}^{N} \alpha_{i}^{*} y_{i} x_{i}\tag{9}\] 再利用KKT条件(不懂就装懂吧嘻嘻)求得: \[b^{*}=y_{j}-(w^*)^Tx_j=y_{j}-\sum_{i=1}^{N} \alpha_{i}^{*} y_{i}\left(x_{i} \cdot x_{j}\right)\tag{10}\] 其中,\(y_{j}\)为任意一个支持向量。
最终的分类超平面为: \[w^{*}\cdot x+b^{*}=0,\sum_{i=1}^{N} \alpha_{i}^{*} y_{i}(x_{i}\cdot x)+b^{*}=0\tag{11}\] 分类决策函数为: \[f(x)=sign(w^{*}\cdot x+b^{*})=\sum_{i=1}^{N} \alpha_{i}^{*} y_{i}(x_{i}\cdot x)+b^{*}\tag{12}\] 最后要bb的是关于支持向量,根据KKT条件里的互补条件\(\alpha_{i}^{*}[y_{i}(x_{i}\cdot w^*+b^{*})-1]=0\):非支持向量必然有\(\alpha_{i}^{*}=0\),只有支持向量才可能出现\(\alpha_{i}^{*}>0\)。
如果回头看\((9)(10)(11)(12)\),所有的非支持向量对SVM没有任何影响,最优超平面以及决策函数都只由少量的支持向量决定,这大概就是支持向量机名称的由来吧~
近似线性可分
上面讨论了完全线性可分的情况,然而在现实情况中,训练数据会有一些outliers,除去这些点后数据是线性可分的。为了处理这种情况,允许SVM分错一些样本。对每个样本点引入松弛因子\(\xi_{i} \geqslant 0\),即样本点的函数间隔只需要大于\(1-\xi_{i}\),放松了限制条件,原优化问题变为: \[ \begin{array}{ll} \min _{w, b, \xi} & \frac{1}{2}\|w\|^{2}+C \sum_{i=1}^{N} \xi_{i} \\ \text { s.t. } & y_{i}\left(w \cdot x_{i}+b\right) \geqslant 1-\xi_{i}, \quad i=1,2, \cdots, N \\ & \xi_{i} \geqslant 0, \quad i=1,2, \cdots, N \end{array}\tag{13} \] 如果样本点严格满足约束,对于损失函数没有贡献;如果不严格满足即\(\xi_{i}>0\),损失函数就会有相应的惩罚。惩罚参数\(C\)控制了一种权衡:既要间隔最大(即\(min\ ||w||\)),又要分对尽可能多的样本点。
类似地,\((13)\)可以通过拉格朗日乘子法转换为对偶问题后再去求解,建议吃饱的同学自己尝试一下。\((13)\)的对偶优化问题是: \[ \begin{array}{ll} \min _{\alpha} & \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)-\sum_{i=1}^{N} \alpha_{i} \\ \text { s.t. } & \sum_{i=1}^{N} \alpha_{i} y_{i}=0 \\ & 0 \leqslant \alpha_{i} \leqslant C, \quad i=1,2, \cdots, N \end{array}\tag{14} \] 此时此刻恰如彼时彼刻,使用普通的二次规划算法或者更高效的SMO求解\((14)\)得到最优的\(\alpha_{i}^{*}\),进而得到软间隔SVM的解: \[ w^{*}=\sum_{i=1}^{N} \alpha_{i}^{*} y_{i} x_{i} \\ b^{*}=y_{j}-\sum_{i=1}^{N} \alpha_{i}^{*} y_{i}\left(x_{i} \cdot x_{j}\right)\tag{15} \] 其中,\(y_{j}\)要满足\(0<\alpha_j<C\)。
非线性可分
上面讨论了线性分类问题,对于非线性可分问题,SVM的思想是做一个变换\(\phi(\vec{x})\),将样本映射到另外一个空间,也许就线性可分了。
由于目标函数和决策函数只依赖于样本对之间的点积,所以无需显式定义变换\(\phi(\vec{x})\),只要定义一个函数\(K(\vec{x_i},\vec{x_j})=\phi(\vec{x_i})\cdot\phi(\vec{x_j})\)提供新空间的样本点的点积即可,\(K\)叫做Kernel
Function。
此时原优化问题为: \[
\begin{array}{ll}
\min _{w, b, \xi} & \frac{1}{2}\|w\|^{2}+C \sum_{i=1}^{N} \xi_{i} \\
\text { s.t. } & y_{i}\left(w^T \phi(x_{i})+b\right) \geqslant
1-\xi_{i}, \quad i=1,2, \cdots, N \\
& \xi_{i} \geqslant 0, \quad i=1,2, \cdots, N
\end{array}
\] 对偶问题为: \[
\begin{array}{ll}
\min _{\alpha} & \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N}
\alpha_{i} \alpha_{j} y_{i}
y_{j}\left(K(x_{i},x_{j})\right)-\sum_{i=1}^{N} \alpha_{i} \\
\text { s.t. } & \sum_{i=1}^{N} \alpha_{i} y_{i}=0 \\
& 0 \leqslant \alpha_{i} \leqslant C, \quad i=1,2, \cdots, N
\end{array}
\] 一种常用的kernel是线性的:\((\vec{u}\cdot\vec{v}+1)^n\),当前空间的\(u\)和\(v\)通过简单的点积映射到了另一个空间;
另一种kernel是高斯核:\(e^{-\frac{||x_i-x_j||^2}{\sigma}}=e^{-\gamma{||x_i-x_j||}^2}\)。
高斯核对应高斯径向基函数分类器,这里有2个参数\(C\)和\(\gamma\)需要调节:惩罚系数\(C\)表示分类器对于误差的宽容度,\(C\)越大表示越不能容忍误差,容易过拟合,按照经验可以在\([10^{-4},10^4]\)间调节;\(\gamma\)控制径向作用范围,\(\gamma\)越大,径向作用范围越小,有可能将每个样本点单独形成一个分类,容易过拟合,\(\gamma\)过小,径向范围过大,容易将2个样本映射为同一个点,无法区分,一般\(\gamma=\frac{1}{样本特征数}\)。另外,这2个参数可以通过交叉验证和grid-search来调整。
扩展
SVM处理多分类问题的方式主要有2种:
- one-against-one
在每2个类之间都构造一个binary SVM,共有\(C_m^2\)个SVM,对新数据采用Voting的方式进行分类。 - one-against-the-rest
对每个类,将其作为正类,其余\(m-1\)个类作为负类,共\(m\)个SVM,对新数据采用winner-takes-all策略。
如果样本不均衡,目标函数中的惩罚项主要由多数类构成,超平面偏向少数类,甚至将所有样本都分在同一侧。
此时目标变为了在不严重损失多数类精度的情况下,在少数类上获得尽可能高的分类正确率。一般来讲有2种做法:
- 数据合成
对少数类样本进行分析并根据其特点人工插值合成新样本添加到数据集中,构成均衡数据集。比较常用的方法是SMOTE(Synthetic Minority Oversampling Technique)。 - 加权SVM
将少数类分错的代价很大,所以在惩罚项中对两个类设置不同的惩罚系数,少数类的系数设置更大,甚至可以对每个样本都设置不同的惩罚系数,此时原优化问题变为: \[ \begin{array}{ll} \min _{w, b, \xi} & \frac{1}{2}\|w\|^{2}+C^+ \sum_{y_i=1} \xi_{i}+C^-\sum_{y_i=-1} \xi_{i} \\ \text { s.t. } & y_{i}\left(w^T \phi(x_{i})+b\right) \geqslant 1-\xi_{i}, \quad i=1,2, \cdots, N \\ & \xi_{i} \geqslant 0, \quad i=1,2, \cdots, N \end{array} \] 对偶问题: \[ \begin{array}{ll} \min _{\alpha} & \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(K(x_{i},x_{j})\right)-\sum_{i=1}^{N} \alpha_{i} \\ \text { s.t. } & \sum_{i=1}^{N} \alpha_{i} y_{i}=0 \\ & 0 \leqslant \alpha_{i} \leqslant C^+, y_i=+1 \\ & 0 \leqslant \alpha_{i} \leqslant C^-, y_i=-1 \end{array} \]

