1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
| class SegmentTree {
public:
struct TreeNode {
TreeNode(int l, int r, int val) : start(l), end(r), val(val), left(nullptr), right(nullptr) {}
~TreeNode() {
if (left) {
delete left;
left = nullptr;
}
if (right) {
delete right;
right = nullptr;
}
}
int start, end, val;
TreeNode* left, *right;
};
TreeNode* buildTree(vector<int>& nums, int l, int r) {
if (l == r) {
return new TreeNode(l, r, nums[l]);
}
int m = l + (r - l) / 2;
TreeNode* lef = buildTree(nums, l, m);
TreeNode* rig = buildTree(nums, m + 1, r);
TreeNode* root = new TreeNode(l, r, lef->val + rig->val);
root->left = lef, root->right = rig;
return root;
}
void update(TreeNode* root, int i, int newVal) {
if (root->start == i && root->end == i) {
root->val = newVal;
return;
}
int m = root->start + (root->end - root->start) / 2;
if (i <= m) {
update(root->left, i, newVal);
} else {
update(root->right, i, newVal);
}
root->val = root->left->val + root->right->val;
}
int query(TreeNode* root, int l, int r) {
if (l == root->start && r == root->end) {
return root->val;
}
int m = root->start + (root->end - root->start) / 2;
if (r <= m) {
return query(root->left, l, r);
} else if (l > m) {
return query(root->right, l, r);
} else {
return query(root->left, l, m) + query(root->right, m + 1, r);
}
return 0;
}
};
|
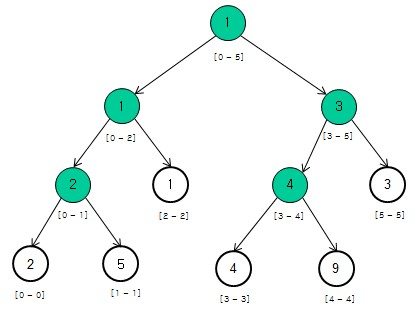 对于每个结点,需要存储起始点、终止点、值、左右指针:
对于每个结点,需要存储起始点、终止点、值、左右指针:
