EI Madrigal's Space
0%

Recursion and Backtracking

Posted on Edited on In
递归与回溯

DFS是一种图的遍历算法:

  1. 从任意结点v开始
  2. 将v标记为已访问
  3. 递归访问v的所有未访问过的邻居

对于树而言, 有向无环, 不用担心结点被访问2次, 因此不需要标记. 无向图可以看作双向有向图, 因此始终是有环的, 也需要标记.

Tree Recursion

递归是计算机科学中一个非常重要的概念，对于斐波那契那种比较简单的递归，分析起来比较容易，但是由于二叉树涉及指针操作，所以模拟下遍历过程中系统栈的情况。
以二叉树中序遍历为例演示： 

1
2
3
4
5
6
7
// 二叉树定义
struct TreeNode {
    TreeNode* left;
    TreeNode* right;
    int val;
    TreeNode(int x) :val(x), left(NULL), right(NULL) {}
};
中序遍历的递归实现：
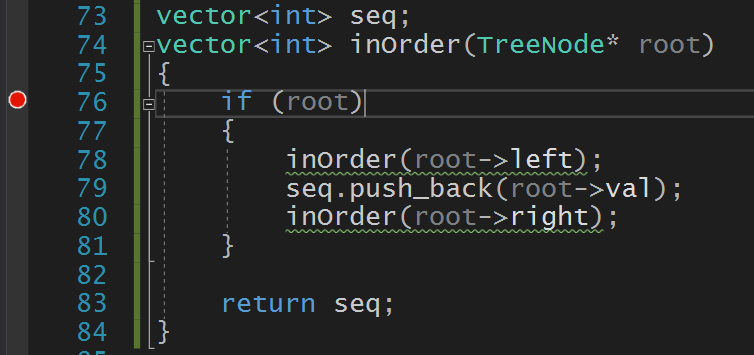
在这里插入图片描述
假设二叉树如图所示：
其中序遍历序列为\(2413\)，可以在VS中用单步调试的方法跟踪相应的变量：
当root==NULL(root指向2的左孩子)时，此时的系统栈（将1和2都压栈，因为中序遍历需要先访问左孩子）：
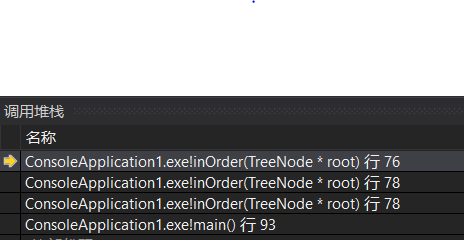
在这里插入图片描述
这时if不成立，执行83行的return语句，接着退栈，回到78行，此时的root指向2(因为此时程序已经来到了新的栈顶)，并且向这个新栈顶返回了一个空的seq：
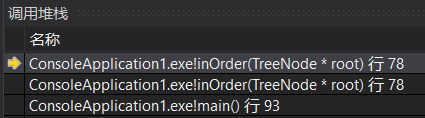
在这里插入图片描述
接着执行79行(因为这是上一个函数return的，所以不会再一次执行78行)，将2存入seq中；
执行80行（root指向4），进而执行78行，root指向4的左孩子，此时的系统栈（很明显可以看到从栈底到栈顶依次存放根结点到当前root结点的路径上的结点）：
在这里插入图片描述
同样，执行return语句，退栈，将seq(里面只有2)返回到这一层，这一层的root指向4，接着将4存入seq；
到80行，调用inOrder()使得root指向4的右孩子，右孩子为空，所以返回并退栈，root重新指向4，此时80行执行完毕，整个if执行完毕，返回seq并退栈，root返回到了2，以2为根结点的子树中序遍历完毕，系统栈：
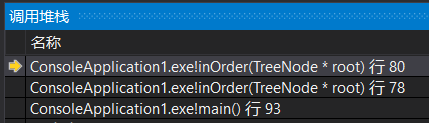
在这里插入图片描述
继续执行，return到78行，root指向1，将1存入seq，以此类推，就可以得到整个的遍历序列。

最关键的是：之所以要递归调用inOrder，就是因为现在还不想访问当前的结点（对于中序，要先找到最左边的结点），所以通过递归的方式将当前暂时不想访问的结点压入系统栈，找到了想访问的结点后，访问它并利用退栈操作返回父结点。
有关树的问题，有一些通用的模板： 

1
2
3
4
5
6
7
8
9
10
11
// one root
func solve(root)
{
    if(root == null)  return ...
    if f(root) return ...

    l = solve(root->left);
    r = solve(root->right);

    return g(root, l , r);
}

1
2
3
4
5
6
7
8
9
10
11
// two roots
func solve(p, q)
{
    if(p == null && q == null)  return ...
    if f(p, q)  return ...

    l = solve(p.child, q.child);
    r = solve(p.child, q.child);

    return g(p, q, l, r);
}

经典递归

除了树这种本身就是递归定义的结构外，还有一些search的问题也可以通过递归解决： 

1
2
3
4
5
6
bool isPalindrome(string s) {
    if (s.length() <= 1)
        return true;
    return s[0] == s[s.length() - 1] &&
        isPalindrome(s.substr(1, s.length() - 2));
}

1
2
3
4
5
6
7
8
9
10
11
12
13
const int NotFound = -1;

int BSearch(vector<string>& v, int start, int stop, string key) {
    if (start > stop) return NotFound;

    int mid = (start + stop) / 2;
    if (key == v[mid])
        return mid;
    else if (key > v[mid])
        return BSearch(v, mid + 1, stop, key);
    else
        return BSearch(v, start, mid - 1, key);
}
1
2
3
4
5
6
int C(int n, int k) {
    if (n == k || k == 0)
        return 1;
    else
        return C(n - 1, k) + C(n - 1, k - 1);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
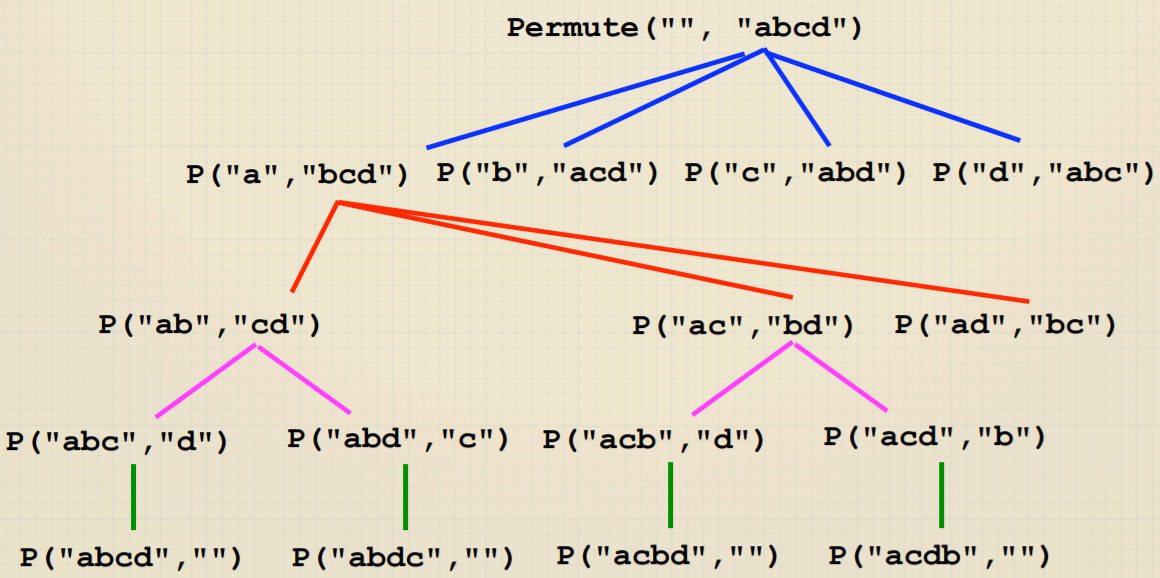
void permute(string soFar, string rest) {
    if (rest == "")
        cout << soFar << endl;
    else {
        for (int i = 0; i < rest.length(); ++i) {
            string next = soFar + rest[i];
            string remaining = rest.substr(0, i) + rest.substr(i + 1);
            permute(next, remaining);
        }
    }
}

// 无重复值
// call stack只有该层所有for循环结束才回退 因此不能传vector<int> path
void permutation(vector<int>& nums, vector<bool>& used, vector<int>& path, vector<vector<int>>& ans) {
    if (path.size() == nums.size()) {
        ans.push_back(path);
        return;
    }

    for (int i = 0; i < nums.size(); ++i) {
        if (used[i]) continue;
        used[i] = true;
        cur.push_back(nums[i]);
        permutation(nums, used, path, ans);
        cur.pop_back();
        used[i] = false;
    }
}

/**
 * 对数组a的[l, r]做全排列
 * 每个数字都要充当第一个
 */
void perm(int a[], int l, int r) {
    if (l == r) {
        for (int i = 0; i < 3; ++i) {
            cout << a[i];
        }
        cout << endl;
        return;
    }
    for (int i = l; i <= r; ++i) {
        swap(a[l], a[i]);  // 第i个元素充当第一个
        perm(a, l + 1, r);  // 剩余元素全排列
        swap(a[l], a[i]);  // 恢复状态，保证下个做第一个元素的状态正确
    }
}

在这里插入图片描述 

1
2
3
4
5
6
7
8
9
10
11
12
void com(vector<int>& nums, int n, int d, int start, vector<int>& cur, vector<vector<int>>& ans) {
    if (n == d) {
        ans.push_back(cur);
        return;
    }

    for (int i = start; i < nums.size(); ++i) {
        cur.push_back(nums[i]);
        com(nums, n, d + 1, i + 1, cur, ans);
        cur.pop_back();
    }
}

1
2
3
4
5
6
7
8
9
10
void subsets(string soFar,string rest) {
    if (rest == "")
        cout << soFar << endl;
    else {
        // add to subset, remove from rest, recur
        subsets(soFar + rest[0], rest.substr(1));
        // do not add to subset, remove from rest, recur
        subsets(soFar, rest.substr(1));
    }
}

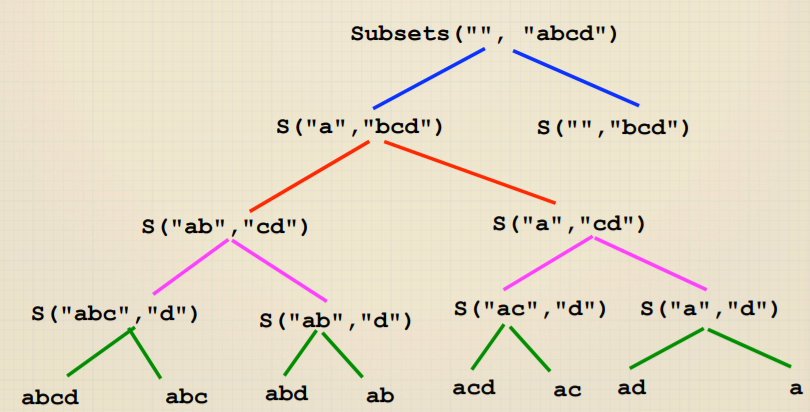
在这里插入图片描述
从递归树可以看到：Permutation和Subsets都是关于选择的问题，树的深度代表选择的次数，每层的宽度代表每次决定时的选项。这种都是Exhaustive Recursion，所以复杂度很高。

Backtracking

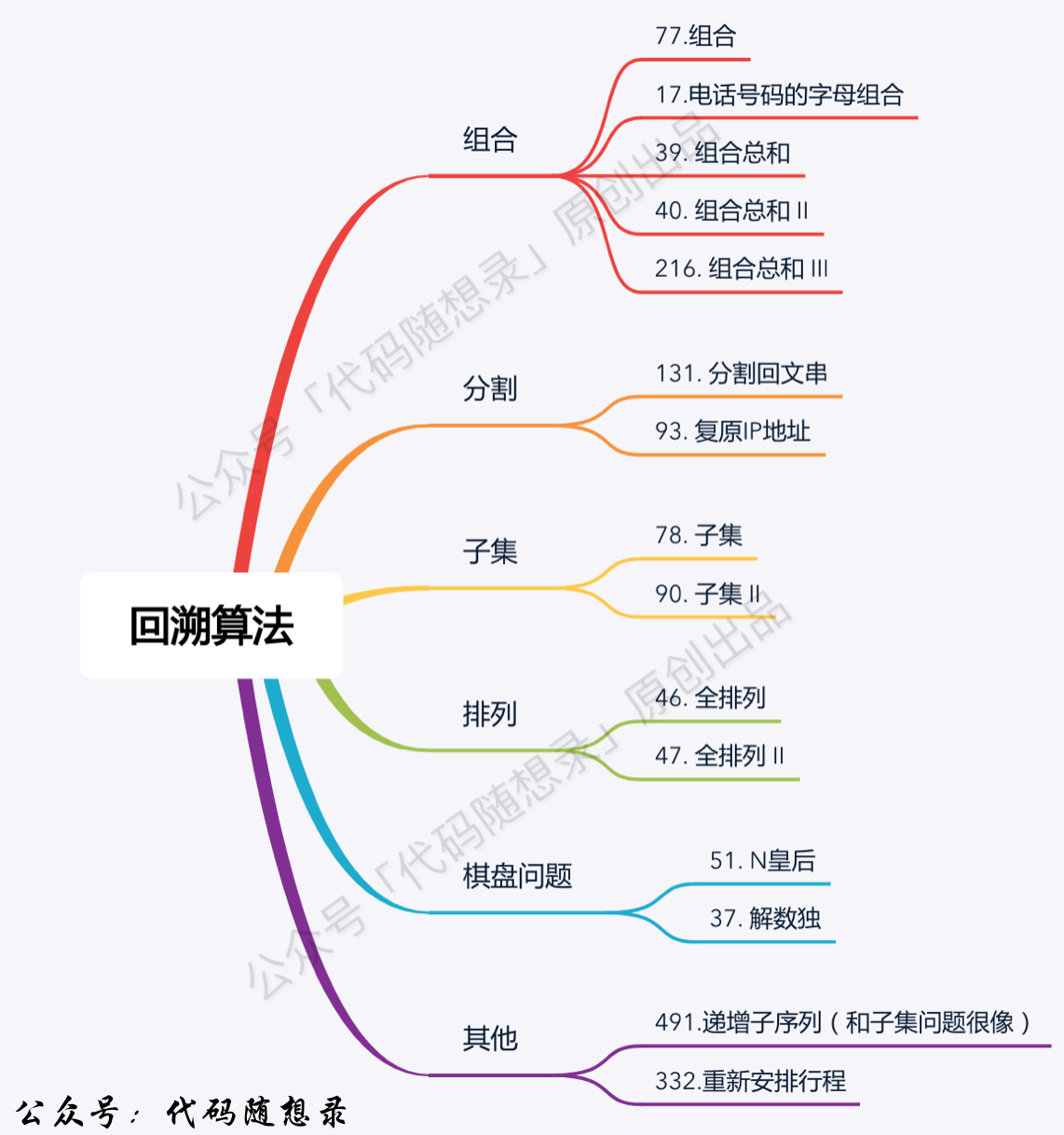
image

主要可以解决组合问题、排列问题、子集问题、字符串切割问题、棋盘问题，这些问题都可以抽象为多叉树的搜索问题

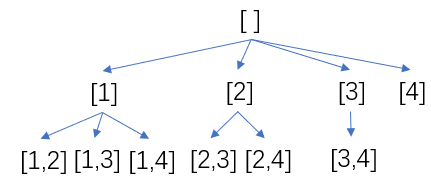
image

回溯用来搜索选择性问题（a series of choices）的所有/部分解，每做一次选择，就递归一次，如果约束条件不满足，需要回退到上一层递归的参数状态。通常在返回上层之前，要将本层节点的状态还原。
通过约束条件的剪枝可以避免对整个搜索空间的穷举，从而提高效率。

三个关键点：

  1. Choice
    明确要做的决定，每次递归代表一次决定，每次的决策结果都保存在这一层的call stack中。
    eg. 遍历二叉树时，当处在某一层的某结点时，下一次递归调用是向左还是向右。
  2. Constraints
    怎样剪枝，当前状态已经invalid，不必再从该状态继续搜索，直接返回。
  3. Goal
    找到target后，就要回溯到上一层，进行其它可能性的搜索。

Pattern： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// backtracking
bool/void solve(configuration conf) {
    if (no more choices)  // base case
        return (conf is goal state);

    for (all available choices) {
        try one choice c:
        // solve from here, if works out, you are done
        if (solve(conf with choice c made))
            return true;
        unmake choice c;   // explore other solutions
    }

    return false;  // tried all choices, no soln found
}

几个例子：

  1. N-Queens
    对照N皇后问题，明确三个关键点：
    1）对于每一列，要做的决定是将Q放在哪一行，每次递归都会进入下一列的决策；
    2）约束条件：不能出现在同一行、同一列、同一斜线；
    3）目标：当在最后一列成功放置Q后，就可以回溯到上一层去探索其它解。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
bool solve(grid<bool>& board, int col) {
    if (col >= board.size()) {
        return true;
    }
    for (int rowToTry = 0; rowToTry < board.size(); ++rowToTry) {
        if (isSafe(board, rowToTry, col)) {
            placeQueen(board, rowToTry, col);
            if (solve(board, col + 1)) {
                return true;
            }
            removeQueen(board, rowToTry, col);
        }
    }
    return false;
}
  1. Sudoku
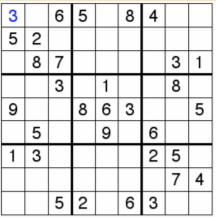
    在这里插入图片描述
    将1-9放入格子，要求每行、每列、每块不能有重复数字。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
bool solve(Grid<int>& grid) {
    // the gird to check, we should check all the grids
    int row, col;

    // all grids assigned successfully
    if (!findUnassigned(grid, row, col)) {
        return true;
    }

    for (int num = 1; num <= 9; ++num) { // options are 1-9
        if (noConflict(grid, row, col, num)) {
            grid(row, col) = num; // try assign
            if (solve(grid)) {
                return true;
            }
            grid(row, col) = UNASSIGNED; // undo and try again
        }
    }
    return false;
}

明白了回溯的基本流程，那么一个问题呼之欲出，什么时候需要回溯，什么时候不需要？

之所以需要回溯，是因为来到\((x,y)\)这个状态后，我们不清楚是否要选择该状态，因此先尝试去选择该状态vis(x,y)=True，然后继续向后搜索dfs(x+i,y+j)。如果发现这样的选择无法得到正确的结果，就尝试不选择该状态vis(x,y)=False，看看能否获得期望的结果。

从实践的角度，当某个状态可能被多条DFS共同访问时（如全排列问题），通常完成一条DFS后需要回溯。当状态只需要访问一次就可以获取最终的结果（如岛屿数量问题），那么无需回溯，这种情况下回溯通常会导致错误的重复计算。

主定理

子问题规模相等 \[ T(N)=aT(\frac{N}{b})+O(N^d) \]

  • \(log_ba<d\rightarrow O(N^d)\)
  • \(log_ba>d\rightarrow O(N^{log_ba})\)
  • \(log_ba=d\rightarrow O(N^dlogN)\)