Percolation

Introduction

这是CS 61B的HW2，具体实现在这里。这个项目是要模拟一个渗滤系统，最终目标是要通过蒙特卡洛方法计算出渗滤系统的阈值，主要会考察对并查集的使用而非实现。
渗滤有很多应用，比较重要的就是复合导电材料：刚开始是绝缘体，将金属作为导电材料逐渐掺入，填充到某临界值后，金属会形成一条导电网格组成的路径，完成从绝缘体到半导体、导体的转变，该临界值就是所谓的渗滤阈值。
模型是一个\(N*N\)的网格图，每个格子有打开和关闭两种状态。如果一个格子是打开的，并且可以通过相邻的某些打开的格子连接到第一行的打开格子，那么该格子的状态就是full。如果最后一行有格子是full，那么系统就会发生渗滤。对于前面的例子，如果金属材料能形成一条从上到下的导电路径，那么就发生渗滤：

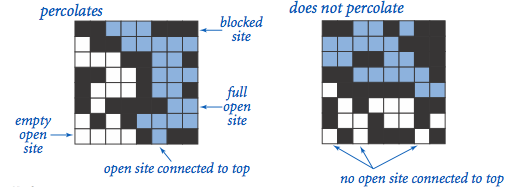
我们感兴趣的是：如果\(N\)足够大，每个格子独立，并且打开的概率是\(p\)，那么会存在一个阈值\(p^*\)，当\(p<p^*\)时，系统几乎不可能发生渗滤；当\(p>p^*\)时，系统几乎一定发生渗滤：

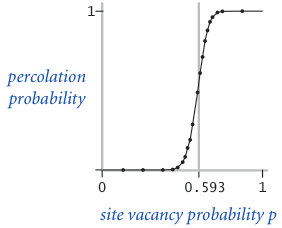
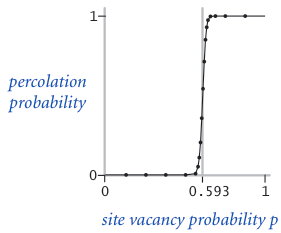
我们的任务就是估算这个\(p^*\)。

渗滤系统建模

模型并不复杂，写一个类Percolation.java专门模拟该系统：

public class Percolation {
   public Percolation(int N)  // create N-by-N grid, with all sites initially blocked
   public void open(int row, int col)  // open the site (row, col) if it is not open already
   public boolean isOpen(int row, int col)  // is the site (row, col) open?
   public boolean isFull(int row, int col)  // is the site (row, col) full?
   public int numberOfOpenSites()  // number of open sites
   public boolean percolates()  // does the system percolate?
}

难点在于要满足规定的时间复杂度：除了构造函数是\(O(N^2)\)，其余方法都必须是\(O(1)\)。
如果采用常规方法判断是否渗滤，那么至少也要遍历最后一行看看有没有full的格子，这样时间\(O(N)\)无法满足要求。
问题就在于第一行和最后一行的格子数太多，减慢了我们的判断效率。那么如果我们在最上面和最下面设置两个虚拟节点，事情就会变得OK：

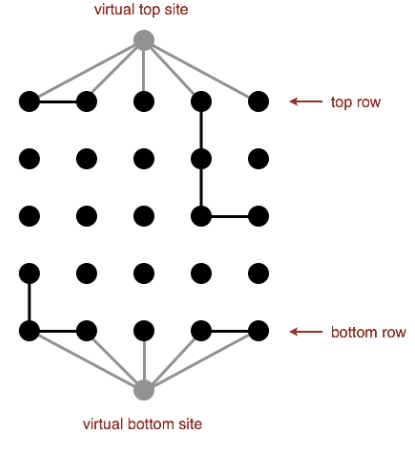
virtualTop负责连接第一行所有打开的结点，virtualBottom负责连接最后一行所有打开的结点，这样我们就把\(N\)个点浓缩成了一个点：

判断某点是否full时，只需要判断该点是否和virtualTop连接；
判断是否渗滤时，只要判断virtualTop和virtualBottom是否连接。

这种解决方案看似很完美，但是有一个问题Backwash：

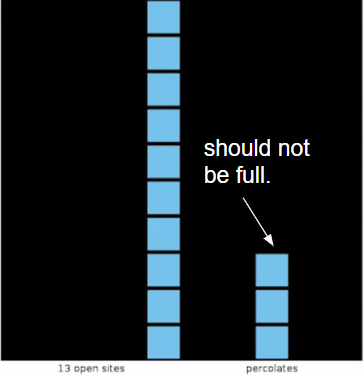
如果已经有一条从上到下的路，那么水流可以通过virtualBottom回流到最后一行已经打开的格子，而这些格子本不应该full。
这个问题的解决有点tricky，开始我是想通过周围格子的状态来判断是否full，即只有周围四个格子之一是full，当前格子才是full。但是如果要在isFull()里递归调用去判断周围格子，那么一定会爆栈；所以要判断周围格子只能通过是否和virtualTop连接，但是只要这个打开的格子在最后一行，就一定要和virtualBottom连接，如此一来只要有其他通路，那么该格子必然还是backwash，进而就会导致其它和该格子相连的也backwash。
举例来说：假如右边3个蓝色格子从上至下编号123，先打开3号，3号周围四个格子都没有和virtualTop连接，因此我们认为3号没有full，这没问题；但是接着打开2号，2号下面的格子（3号在最后一行且打开，必然和virtualBottom连接，即也和virtualTop连接）是和virtualTop连接的，因此我们判断2号是full，这显然错误。

没法用逻辑优化的时候，就应该转向用空间去优化。我们可以在开一个并查集，这个集合最多只包含virtualTop和地图中的所有格子，而将virtualBottom排除在外。判断full时，只要当前格子在新并查集中与virtualTop连接，那么必然full。

Monte Carlo Simulation

为了估算阈值，需要做\(T\)次独立重复实验：

所有格子都设置为关闭；
随机选取一个关闭的格子，打开它，重复直至系统渗滤。

那么这次试验的\(p^*\)就是打开格子数/总数。

取\(T\)次实验的平均值，可以得到更加精确的阈值；标准差\(\sigma\)展示了结果的波动程度： \[ \mu = \frac{x_1 + x_2 + … + x_T}{T},\sigma^2 = \frac{(x_1 - \mu)^2 + (x_2 - \mu)^2 + … + (x_T - \mu)^2}{T-1} \] 当\(T\)足够大，\([\mu - \frac{1.96\sigma}{\sqrt{T}}, \mu + \frac{1.96\sigma}{\sqrt{T}}]\)提供了95%的置信度。

这部分的实现很简单：

public class PercolationStats {
   public PercolationStats(int N, int T, PercolationFactory pf)  // perform T independent experiments on an N-by-N grid
   public double mean()  // sample mean of percolation threshold
   public double stddev()  // sample standard deviation of percolation threshold
   public double confidenceLow()  // low endpoint of 95% confidence interval
   public double confidenceHigh()  // high endpoint of 95% confidence interval
}