Optimization Methods in Deep Learning

Background

深度神经网络的训练过程主要通过求解一个特定的优化问题来实现，然而由于该问题是一个复杂的高维非线性优化问题，并且不同的网络结构差异很大，不能将传统的优化方法直接使用。即使数据集和网络结构完全相同，不同的优化算法也可能导致完全不同的收敛效果。实际应用的一些简单方法虽然行之有效，但现有理论无法充分解释其有效性，超参数的不断增加也给优化增加了不少难度。如何确保算法收敛、如何尽快收敛以及能否收敛到全局最优一直是困扰学术界和工业界的问题。如果能够用优化理论去解释神经网络的训练行为，对于深度学习的推广应用将会起到巨大的推动作用。

对于有监督学习，给定包含n个样本的训练集\(\{(\mathbf{x}_1, y_1), \ldots, (\mathbf{x}_n, y_n)\}\)，\(\mathbf{x}\)表示样本的特征向量，\(y\)表示该样本对应的标签。我们的任务是利用样本信息来预测相应的标签，使预测值尽可能接近真实标签。如果用深度学习来完成这个任务，就需要通过调整神经网络的参数（权重W和偏差b）来近似数据背后的函数映射关系，这个关系往往是高度非线性的，网络越深表达能力也就越强，逼近效果的精度也就更高，因此网络结构很可能是极其复杂的。

为了衡量预测值和真实值之间的接近程度，通常需要采用某种距离度量方式\(l\)，\(l\)一般设计为可微的，接着用一些优化算法去最小化该目标函数。因此优化问题变为寻找最佳的参数使得\(l\)最小，在不考虑正则项的情况下有： \[ \mathop{\mathrm{min}}_f \frac{1}{n} \sum_{i=1}^n l(f(\mathbf{x}_i), y_i) \] \(f\)就是我们从输入到输出的映射函数，\(l\)通常也叫损失函数，衡量预测值\(f(x_i)\)和真实标签\(y_i\)的差距，比如回归问题中经常使用的平方损失函数\(l=||f(x_i)-y_i||^2\)。

需要注意的是：深度学习中的优化问题与传统意义上的优化问题有所差别。传统的优化问题需要尽可能找到目标函数的最值，而深度学习的最终目的是为了预测未知的数据，而不是将训练数据上的损失降到最低。我们定义的损失函数\(J(\Theta)\)衡量的是当前模型参数\(\Theta\)在训练集上的优劣，然而，最小化训练误差并不意味着模型的泛化误差也会最小，为了降低泛化误差我们还需要关注过拟合问题，因此损失函数往往要加上正则项。统计学上称为经验风险最小化，即由于无法获得全部数据，所以只能用经验风险作为实际风险的近似。非常有意思的是：尽管大多数神经网络都是严重过参数化的，但是反而有着比较不错的泛化能力，这与传统的机器学习观点是矛盾的，泛化理论也需要更加深入的研究。

深度学习中的\(f\)通常是多层的复合函数，由于太复杂而无法求出解析解，所以要用数值优化算法去求解。实际中主流的深度学习优化算法都利用梯度下降来求解，梯度下降是深度学习优化算法的基础，尽管目前已经很少直接使用，但它却是其他高级优化算法的基石： 假设网络的参数为\(x=(x_1,x_2,...,x_d)^T\)，优化的目标函数为\(f\)，那么\(f\)的梯度为： \[ \nabla f(\mathbf{x}) = \bigg[\frac{\partial f(\mathbf{x})}{\partial x_1}, \frac{\partial f(\mathbf{x})}{\partial x_2}, \ldots, \frac{\partial f(\mathbf{x})}{\partial x_d}\bigg]^\top \] 每个元素对应着目标函数在该方向上的变化率，因此只要沿着梯度的反方向就可以使目标函数减小得最快：\(\mathbf{x} \leftarrow \mathbf{x} - \eta \nabla f(\mathbf{x})\)，\(\eta\)是一个被称为学习率的超参数，用来控制每一步的大小。\(\eta\)过小，收敛过程极度缓慢；\(\eta\)过大，可能造成损失函数在最小点附近波动甚至发散。学习率的调整是神经网络训练过程中一个重要的调整参数，常常使人头痛不已，因此也出现了很多学习率自适应调整的算法，将在下面深入分析这些算法的优劣。

有了优化模型及最基础的求解方法后，我们需要对其性质和优缺点进行分析，以便于后续的改进。深度学习的优化问题大多是非凸的，因此存在很多挑战：

1. 局部最优：对于凸优化问题，局部最优即是全局最优。然而对于非凸问题，当损失函数到达局部最优点时，\(J(\Theta)\)的梯度为0，\(\Theta\)无法继续更新，损失函数无法继续下降；
2. 鞍点：该点既不是局部最小也不是全局最小，但是该点的梯度消失，无法继续更新；
3. 梯度消失/爆炸：由于初始值和激活函数选择不当 (如sigmoid)，当梯度反向回传时，可能在某一层求导后梯度值很小/很大，导致训练速度极其缓慢。因此初始值的选择通常采用很小的随机数，避免收敛到比较差的区域，激活函数通常也会选择ReLU，避免梯度消失问题。

局部最小和鞍点示意图如下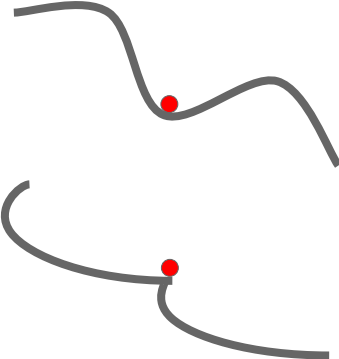： 尤其在高维空间中，鞍点的问题变得更加严重：假设\(\Theta\)是一个k维向量，\(J(\Theta)\)的海森矩阵就有k个特征值，其梯度为0的点有可能是局部最小（特征值均为正）、局部最大（特征值均为负）或者是鞍点（特征值有正有负）。高维空间中特征值有正有负的概率很大，因此鞍点出现的可能性远大于局部最优点出现的可能性，并且鞍点周围的平坦区域可能很大，需要增加噪声扰动来逃离鞍点。

由于上述问题的存在，通常很难找到\(J(\Theta)\)的全局最优解，但实际上为了减少过拟合的风险我们并不需要训练集上的全局最优，经典的梯度下降就可以带来足够的局部最优。

分析完优化模型本身的问题，再来看看最基础的GD的问题：目标函数通常是训练集中所有样本的损失的平均值，故目标函数的梯度为： \[ \nabla f(\mathbf{x}) = \frac{1}{n} \sum_{i = 1}^n \nabla f_i(\mathbf{x}) \] 如果用Full-batch GD，那么每次迭代每个参数的梯度计算的时间复杂度为\(O(n)\)，对于大规模数据，这样的更新速度显然无法令人忍受。

学习率的选择是一项重要的调参工作，因此学习率的自适应变化就成为了研究热点之一，一些二阶方法应运而生，我们首先来看看牛顿法该如何解决这个问题。

对于损失函数\(f\)，利用泰勒展开式有： \[ f(\mathbf{x} + \boldsymbol{\epsilon}) = f(\mathbf{x}) + \boldsymbol{\epsilon}^\top \nabla f(\mathbf{x}) + \frac{1}{2} \boldsymbol{\epsilon}^\top \nabla^2 f(\mathbf{x}) \boldsymbol{\epsilon} + \mathcal{O}(\|\boldsymbol{\epsilon}\|^3) \] 式中的\(\nabla^2 f(\mathbf{x})\)即\(d*d\)海森矩阵，存储了函数的二阶偏导数。为了求得\(f\)的最小值，令上式对\(\epsilon\)求导得0，有：\(\boldsymbol{\epsilon}=-\nabla f(\mathbf{x})H^{-1}\)，即每次的参数更新为\(\mathbf{x} \leftarrow \mathbf{x} - \nabla f(\mathbf{x})H^{-1}\)。二阶近似利用了损失函数的曲率信息，即如果曲率比较小，那么这步更新就会比较大，反之则更新较小。这里没有了学习率，而是通过“梯度的梯度”自动调整步幅，看起来比一阶的梯度下降要好一些。

然而深度学习的参数空间往往十分巨大，因此存储和计算海森矩阵的逆是不现实的，这也是牛顿法无法在DNN中使用的重要原因。为了缓解这个问题，学术界提出了一些拟牛顿法如L-BFGS等试图去降低存储消耗，但是计算代价仍然很高。

从以上的分析可以看到：无论是Full-batch GD还是牛顿法，都存在计算消耗大等问题，不适用于深度学习任务的大规模数据集训练，因此已经很少被直接用在深度学习模型中。为了处理这些问题，学术界提出了很多替代的优化算法，因此接下来我将调研分析当前常用的深度学习优化算法 (SGD/Adam...)的优缺点，并结合实例及前沿研究进行相关讨论。 ## Popular Algorithms 优化算法在神经网络的训练中有着举足轻重的作用，选择合适的优化算法可以使得损失函数收敛地更快，同时收敛到更好的区域。目前比较流行的算法有下面几种： ### 1 SGD 尝试用mini-batch的梯度平均值作为整体梯度的无偏估计，参数的更新非常简单，沿着梯度的反方向即是loss下降最快的方向： \[ x_{t+1}=x_t-\alpha\nabla f(x_t) \] 如果是Batch GD并且学习率足够小时可以保证损失函数单调不增。实际使用时一般会采用学习率递减策略保证模型收敛。

实现也非常简单：

x -= lr * grads

SGD存在几个问题：

首先，如果loss对于不同参数的敏感程度不同，那么收敛过程会在敏感参数方向上抖动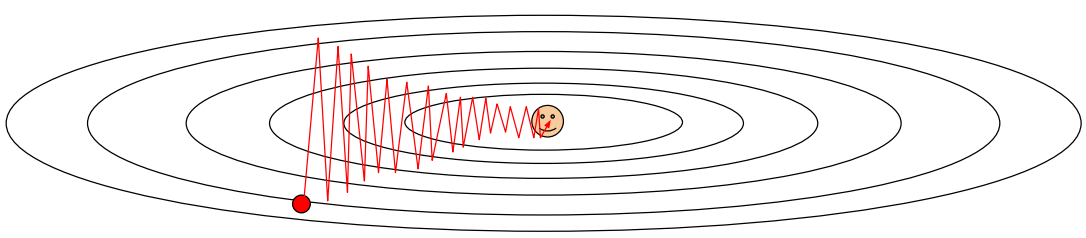： 对于非常大的参数空间，可能会收敛到不同的区域。 其次，如果loss函数有局部最优或者鞍点，这些点上梯度为0，无法收敛到全局最优； 最后，如果采用mini-batch，那么计算出的梯度值是有噪声的，意味着收敛过程可能会是非常曲折的，也即需要更多时间。 ### 2 SGD+Momentum 为了解决SGD的问题，有学者提出了带有动量的SGD，其思想也很简单：更新参数时不仅考虑当前的梯度方向，还要考虑历史累积梯度方向，如果两者方向一致，那么这一步更新幅度就会增大；如果不一致，就会减弱沿当前梯度的下降幅度。 \[ v_{t+1}=\rho v_t+\nabla f(x_t) \\ x_{t+1}=x_t-\alpha v_{t+1} \] \(\rho\)可以看作是对历史梯度的衰减，一般取0.9。

带有动量的SGD实现：

v = rho * v + grads
x -= lr * v

这样就解决了SGD的三个问题： 首先，由于历史梯度的存在，朝敏感方向步进的数量就会减少，会更加平滑的向最优点前进，减小了震荡，加速收敛； 其次，对于局部最优点，虽然当前梯度为0，但是依靠历史梯度可以越过该点继续下降； 最后，梯度噪声引起的震荡可以通过历史梯度互相抵消。 ### 3 Nesterov Momentum Nesterov Momentum由SGD+Momentum衍生而来，SGD+Momentum是将当前点的梯度和速度结合起来，而Nesterov Momentum则是将当前点的速度和下一个近似点的梯度结合起来，意味着我们不是在当前位置去看未来，而是多看了一步，在稍远一些的下一步看未来，可以提前调整步进大小： 所以Nesterov Momentum的更新规则为： \[ v_{t+1}=\rho v_t-\alpha\nabla f(x_t+\rho v_t) \\ x_{t+1}=x_t+v_{t+1} \] 通常我们希望针对\(x_t\)计算梯度，通过简单的变量替换，得到新的更新规则： \[ v_{t+1}=\rho v_t-\alpha\nabla f(x_t) \\ x_{t+1}=x_t+v_{t+1}+\rho(v_{t+1}-v_t) \] Nesterov的实现：

v_prev = v
v = rho * v - lr * grads
x += (1 + rho) * v - rho * v_prev

### 4 AdaGrad 前面的几种方法都是设置了一个全局的学习率，AdaGrad则通过引入二阶动量使得学习率可以针对每个参数自适应地取值：对于更新频繁的参数，已经有了很多认知，不希望因为单个样本影响太大，所以学习率可以小一些；对于更新稀疏的参数，希望从偶尔出现的能更新该参数的样本中多获得一些信息，所以学习率可以设置地大一些。为了了解参数更新的频繁程度，引入二阶动量——每个维度上历史梯度值的平方和： \[ grad\_squared +=\nabla^2 f(x_t) \\ x_{t+1}=x_t-\cfrac{\alpha\nabla f(x_t)}{\sqrt{grad\_squared+10^{-7}}} \] 此时的学习率实质上是\(\cfrac{\alpha}{\sqrt{grad\_squared}}\)，为了避免除0，一般分母加上一个很小的平滑项。如果某个参数更新频繁，那么grad_squared就会增大，学习率也就越小。

AdaGrad的实现：

grad_sq += grads**2
x -= lr * grads / (numpy.sqrt(grad_sq) + eps)

AdaGrad的问题在于随着grad_squared单调递增，学习率最终会单调衰减到0，意味着很可能会提早终止训练过程。 ### 5 RMSProp/AdaDelta 为了缓解AdaGrad的学习率变化过于激进的问题，二阶动量的计算不累积全部的历史梯度，只关注过去某段时间内的梯度变化，用指数移动平均值来表示过去某时间段的二阶动量的均值： \[ grad\_squared=decay\_rate*grad\_squared+(1-decay\_rate)\nabla^2 f(x_t) \\ x_{t+1}=x_t-\cfrac{\alpha\nabla f(x_t)}{\sqrt{grad\_squared+10^{-7}}} \] decay_rate是一个超参数，一般取值0.9。

RMSProp的实现：

grad_sq = decay * grad_sq + (1 - decay) * grads**2
x -= lr * grads / (numpy.sqrt(grad_sq) + eps)

因此，RMSProp仍然是通过梯度的大小来调整每个参数的学习率，不过现在学习率不会单调递减。

6 Adam

Adam的出现是集成了一阶动量思想和AdaGrad等的二阶动量思想，即Adaptive Momentum： \[ m_{t+1}=\beta_1m_t+(1-\beta_1)\nabla f(x_t)\\ V_{t+1}=\beta_2V_t+(1-\beta_2)\nabla^2 f(x_t)\\ x_{t+1}=x_t-\cfrac{\alpha m_{t+1}}{\sqrt{V_{t+1}+10^{-7}}} \] 由于m和V初始化为0，所以开始的几次迭代会偏向取值0，为了弥补这一缺点，又引入了偏差纠正项，完整的Adam算法如下： \[ m=\beta_1m+(1-\beta_1)\nabla f(x_t)\\ m_t=\cfrac{m}{1-\beta_1^t}\\ V=\beta_2V+(1-\beta_2)\nabla^2 f(x_t)\\ V_t=\cfrac{V}{1-\beta_2^t}\\ x_{t}=x_{t-1}-\cfrac{\alpha m_{t}}{\sqrt{V_{t}+10^{-7}}} \] Adam的实现：

m = beta_1 * m + (1 - beta_1) * grads
m_t = m / (1 - beta_1**t)
v = beta_2 * v + (1 - beta_2) * grads**2
v_t = v / (1 - beta_2**t)
x -= lr * m_t / (numpy.sqrt(v_t) + eps)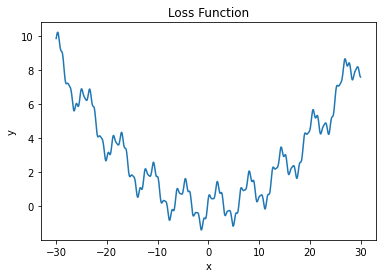

如果Adam再加上Nesterov的向后看一步的思想，就是Nadam算法。 ## Experiment 为了对上述算法有更加直观的认识，同时在部分程度上比较不同算法的性能，构造一维函数\(f(x)\)作为损失函数，其表达式如下： \[ f(x)=0.01x^2+sin(x)+\frac{1}{3}cos(3x)+\frac{1}{5}sin(5x)+\frac{1}{7}cos(7x) \] 这个损失函数含有大量的局部最小点以及悬崖，如图所示： 为了公平起见，比较时将x的初始值设为-29，每种算法的迭代次数均设置为300次，学习率均设置为0.1，迭代过程如下图所示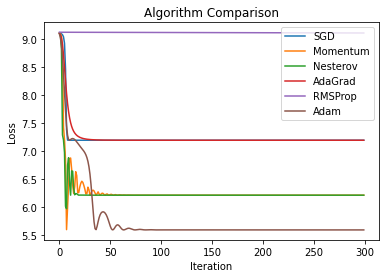： 最终的收敛结果如下表所示： | 算法 | 最终x | 最终损失 | | -------- | ------ | -------- | | SGD | -27.98 | 7.19 | | Momentum | -24.00 | 6.21 | | Nesterov | -24.00 | 6.21 | | AdaGrad | -27.98 | 7.19 | | RMSProp | -28.95 | 9.10 | | Adam | -26.46 | 5.59 |

从上图和上表可以看到：Adam算法在前期收敛很快，并且最终效果最好，是综合性能最佳的算法；带动量的SGD能够越过一些局部极小值，在没有精细调参的情况下一度达到了和Adam类似的效果；AdaGrad开始时的梯度很大，但是由于学习率过早地减小，最终效果并不出众；这些结果进一步佐证了之前对各种算法的分析。

如果将学习率设置为0.01，对比如下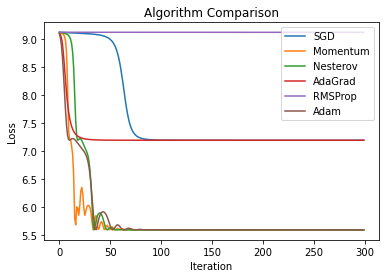： 可以看到：精调后的Momentum、Nesterov和Adam的效果几乎不相上下，这只是初步调整了学习率参数，如果通过验证集更加精细地调整超参数的值，那么SGD+Momentum完全可以达到甚至超越Adam的表现，当然这也需要人为付出更多的努力，Adam这个烦恼则小得多。

# -*- coding: utf-8 -*-
"""
Created on Sun Apr 11 18:31:58 2021

@author: Jingtao Ren
"""

import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt


a = tf.constant(3.0)
b = tf.constant(5.0)
c = tf.constant(7.0)
d = tf.constant(0.1)
x = tf.Variable(initial_value=-29.0, name="x", dtype=tf.float32)


def plot_f():
    x = np.linspace(-30, 30, 1000)
    # y = -20.0 * np.exp(b * np.abs(x)) - np.exp(np.cos(c * x)) + 20.0 + np.exp(1)
    y = (0.1 * x) ** 2 + np.sin(x) + np.cos(a * x) / a + np.sin(b * x) / b + np.cos(c * x) / c
    plt.xlabel('x')
    plt.ylabel('y')
    plt.title('Loss Function')
    plt.plot(x, y)
    plt.show()


def plot_train(y):
    x = np.arange(300)
    labels = ['SGD', 'Momentum', 'Nesterov', 'AdaGrad', 'RMSProp', 'Adam']
    plt.figure()
    plt.xlabel('Iteration')
    plt.ylabel('Loss')
    plt.title('Algorithm Comparison')
    for i in range(6):    
        plt.plot(x, y[i], label=labels[i])
        plt.legend()
    plt.show()


def loss():
    # y = a * tf.exp(b * tf.abs(x)) - tf.exp(tf.cos(c * x)) - a + tf.exp(tf.constant(1.0))
    y = tf.pow(d * x, 2) + tf.sin(x) + tf.cos(a * x) / a + tf.sin(b * x) / b + tf.cos(c * x) / c
    return (y)


def minimize(optimizer, iters = 300):
    y = []
    # optimizer = tf.keras.optimizers.SGD(learning_rate=0.1)
    for i in tf.range(iters):
        optimizer.minimize(loss, [x])
        y.append(loss())
    tf.print("Final x = ", x)
    tf.print("Final Loss = ", loss())
    return y


if __name__ == "__main__":
    # plot_f()
    ops = [tf.keras.optimizers.SGD(learning_rate=0.1), tf.keras.optimizers.SGD(learning_rate=0.1, momentum=0.9),
           tf.keras.optimizers.SGD(learning_rate=0.1, momentum=0.9, nesterov=True), tf.keras.optimizers.Adagrad(learning_rate=0.1),
           tf.keras.optimizers.Adadelta(learning_rate=0.1, rho=0.9), tf.keras.optimizers.Adam(learning_rate=0.1)]
    y = []
    for i in range(6):
        x.assign(-29.0)
        y.append(minimize(ops[i]))
    plot_train(y)

当然，这个实验非常简单，损失函数形式是一维的，实际中的网络模型参数的数量可能达到百万级别，超高维情况下算法的效率、鲁棒性以及模型最终的泛化能力才是我们真正关心的。

最后贴2张神图总结下： ## Research Adam虽然是集大成者，而且也被推荐为起始的默认优化算法，但是一些Paper揭示了Adam的一些问题。 ### 1 过拟合 Berkeley在NIPS 2017的一篇文章指出：如果一个问题有多个全局极优，即使从相同的初始值出发，不同的优化算法也会得到完全不同的结果。文章构造了一个简单的线性可分的二分类问题，证明了SGD在这种情况下测试误差为0，而AdaGrad等自适应方法会把所有的测试样例分为正类，泛化能力极差，也就是根本不能工作。

随后作者又用VGG+BN+Dropout的网络结构在CIFAR-10数据集上进行了实验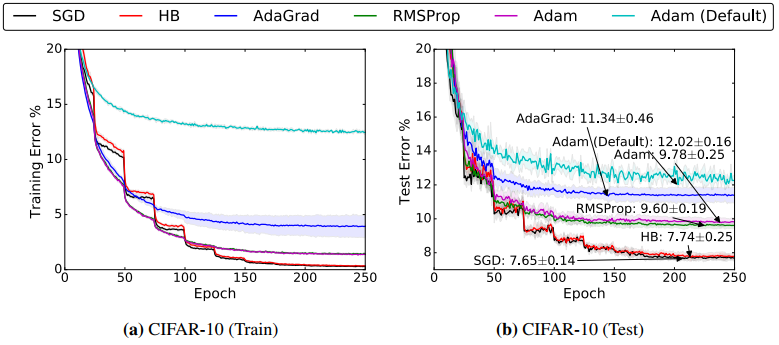： 可以看到：前期训练中Adam有优势，但SGD的泛化能力确实比Adam要好。

最后，为了彻底黑化Adam，文章又用了文本数据集和一些NLP模型做了实验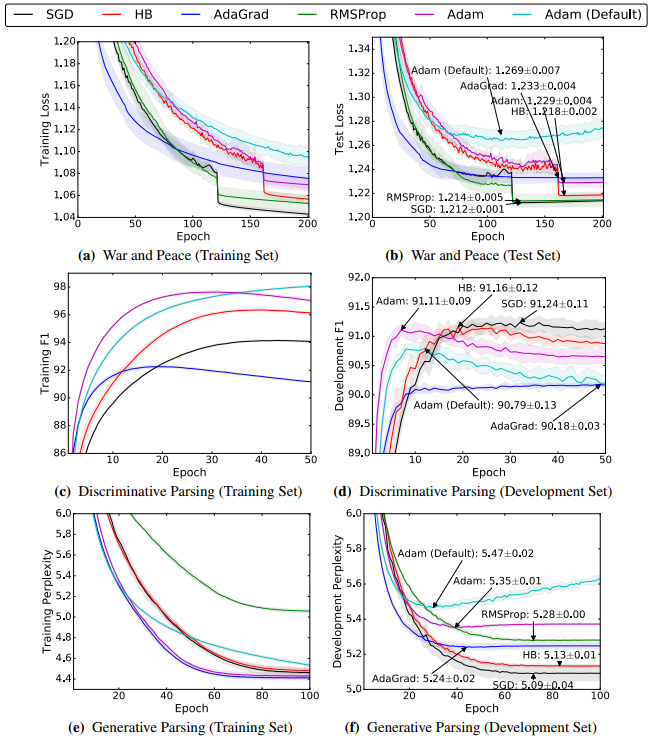： 即便有时候自适应方法的训练loss会更低，但SGD的泛化能力都无一例外地胜过了自适应的方法。自适应方法在训练初期速度很快，但是后期表现平平。

泛化能力差的原因在于：自适应方法倾向于关注稀疏的特征，因为这些特征对于训练样例的鉴别是很有效的，尤其在训练样例数少而特征较多的数据集中，但是这些特征其实并非关键特征，这样自适应学习率算法出现过拟合的风险就会增大，导致泛化能力不佳，最终的收敛效果不如传统的SGD。 ### 2 二阶动量波动 Google的一篇文章从数学上证明了在某些特定情况下Adam可能不收敛，因为二阶动量取的是某个时间窗口的变化，所以\(V_t\)的变化可能会剧烈震荡，尤其在高维情况下，梯度的方差可能随时间波动很大，导致学习率震荡，模型无法收敛。这也是为什么一般\(\beta_2\)要取0.999这么大的值，避免二阶动量有太大波动。

一般认为Adam默认的\(\beta_1\)和\(\beta_2\)不需要调整，采用默认的0.9和0.999即可。但是这两个超参如果不按这样设置，Adam可能永远不会收敛到最优值。文章从数学上证明了对任意的\(\beta_1,\beta_2\in[0,1),\beta_1<\sqrt{\beta_2}\)，都存在一个随机的凸优化问题使得Adam不能收敛到最优解。

为了避免二阶动量的剧烈震荡，文章对其进行了控制，提出了一个新算法AMSGrad确保模型收敛，\(V_t=max(V_{t-1},\beta_2V_{t-1}+(1-\beta_2)\nabla^2 f(x_t))\)。

作者随后通过人造数据和真实数据进行了实验：

人造数据上的结果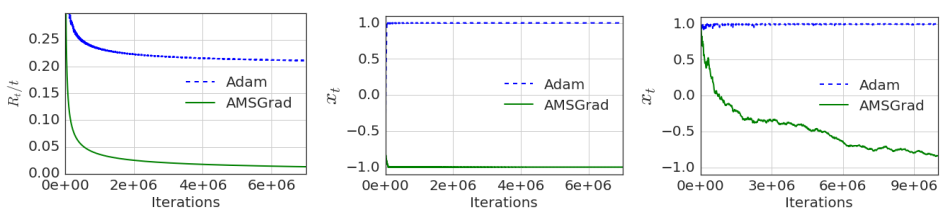： 很显然在Adam没有找到最优解的这些数据上，改进后的算法都表现良好。

在MNIST上的效果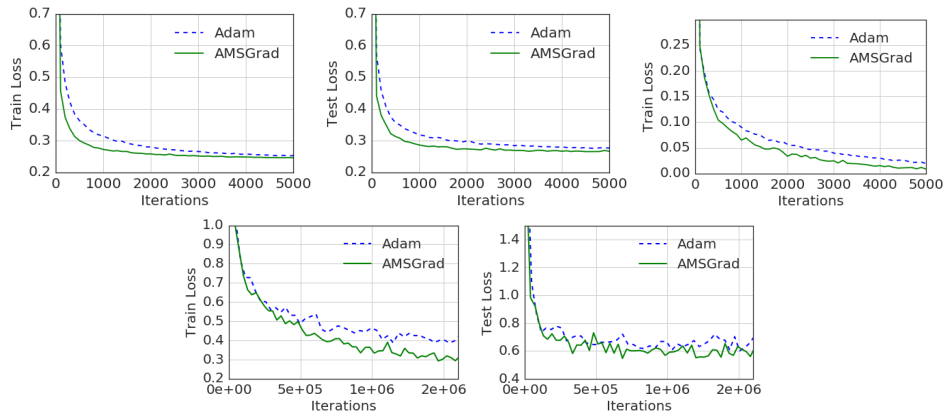： 这篇文章最终获得了2018年ICLR最佳论文，但是引起了很大争议。主要原因在于其构造的令Adam失效的数据在实际情况中出现的概率极低，即使出现也会在数据预处理时被筛掉，因此并没有特别广泛的实际用处。另外，文章过于强调训练集上的损失函数值，甚至有人通过复现表明文章提出的AMSGrad算法在测试数据上表现很差，与原文中的某些结论相互矛盾。 ### 3 学习率下降 arXiv上的一篇文章通过在CIFAR-10上的实验证明Adam在一些情况下虽然速度快，但收敛效果没有SGD好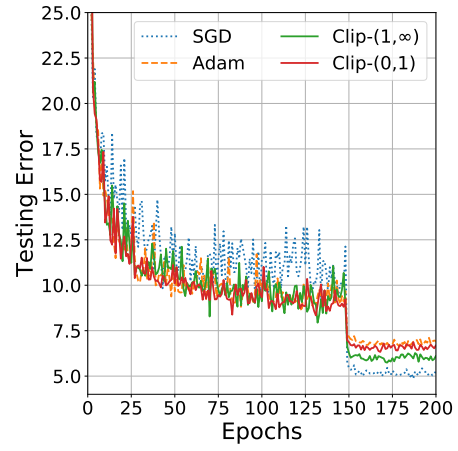： 文章通过实验发现主要原因在于后期Adam的学习率过低，影响了最终效果。文章尝试通过控制学习率下界，提高了最终收敛效果。

既然Adam后期有问题，那么一个自然的改进就是前期训练使用Adam，用来快速减小loss；后期训练转换为SGD，用稍慢的速度寻找更佳的解甚至是最优解。但是这样也会引入新的问题：在什么时刻切换？切换为SGD后的学习率又该如何设置？

文章提出了SWATS(Switches from Adam to SGD)策略来解决上面2个问题，在CIFAR-10和CIFAR-100数据集上实验效果看着还不错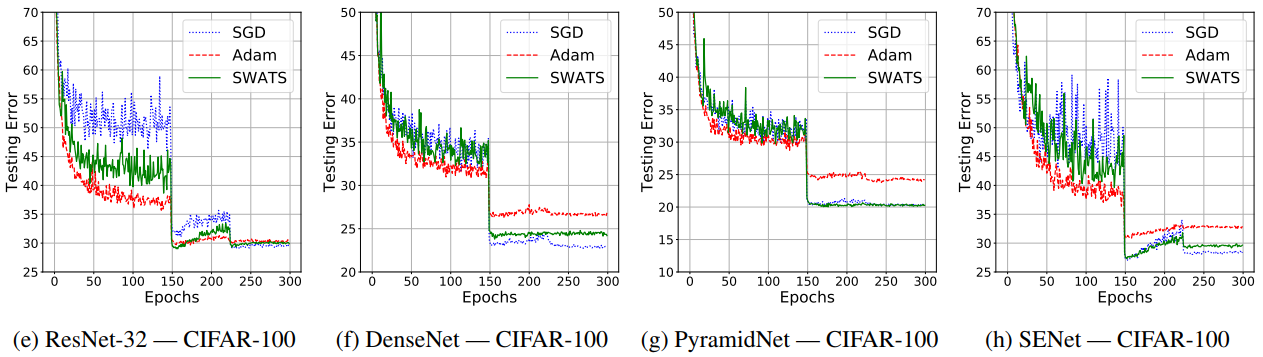： 这些文章都采用了一些比较极端的数据去探索Adam的不适情况，然而实际中遇到这些极端情况的概率并不大，因此Adam并不失为首选尝试。通过上面的讨论可以看到：SGD和Adam各有优劣，精调后的SGD一般最终会收敛到更好的效果；Adam在训练前期收敛速度快，在稀疏数据上表现更好，对超参不敏感，不需要十分精细的调参。

如果对优化算法不熟悉，可以先尝试SGD+Nesterov Momentum或者Adam；如果对某个优化算法很精通，那么调参就会相对容易些。如果资源足够，也可以尝试L-BFGS等二阶优化方法。另外，选择之前要充分了解数据的性质，对于比较稀疏的数据可以优先尝试学习率自适应调整的算法。

Reference

[1] CS231n: Convolutional Neural Networks for Visual Recognition. lecture 8, Stanford University.
[2] The Marginal Value of Adaptive Gradient Methods in Machine Learning. NIPS'17
[3] On the Convergence of Adam and Beyond. ICLR'18
[4] Improving Generalization Performance by Switching from Adam to SGD. arXiv
[5] Optimization methods for large-scale machine learning. SIAM Review, 2018.
[6] Optimization for deep learning: theory and algorithms. arXiv, 2019.
[7] Understanding Black-box Predictions via Influence Functions. ICML'17.
[8] Understanding Deep Learning Requires Rethinking Generalization. ICLR'17.