图和网络
图是一些工程问题的抽象,比如电路网络:
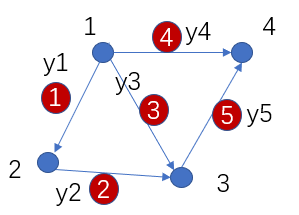
我们可以用\(A_{54}\)表示图中的信息,每行代表一条边,每列代表一个结点,1表示电流流入,-1表示流出:
\[
A=\begin{bmatrix}
-1 & 1 & 0 & 0 \\
0 & -1 & 1 & 0 \\
-1 & 0 & 1 & 0 \\
-1 & 0 & 0 & 1 \\
0 & 0 & -1 & 1 \\
\end{bmatrix}
\] \(edge3=edge1+edge2\),前三行线性相关,在图中表现为形成环路。
我们比较关注\(A\)的零空间,也即如何组合各列以得到零列\(Ax=0\),即: \[
Ax=\begin{bmatrix}
x_2-x_1\\
x_3-x_2\\
x_3-x_1\\
x_4-x_1\\
x_4-x_3\\
\end{bmatrix}=\begin{bmatrix}
0\\
0\\
0\\
0\\
0\\
\end{bmatrix}
\] 根据前面的学习,\(dim(N(A))=n-r(A)=4-3=1\),并且可以求出零空间:\(x=c\begin{bmatrix}
1\\
1\\
1\\
1\\
\end{bmatrix}\),如果\(x_i\)表示结点\(i\)的电势,那么从结果可以看出来四个点等电势,一旦确定某个点的电势(接地为0),即可确定其余各点。
再研究一下\(A\)的左零空间,即\(A^Ty=0\),\(dim(N(A^T))=m-r(A)=5-3=2\),不妨看看转置后的鬼样子:
\[
\begin{bmatrix}
-1 & 0 & -1 & -1 & 0 \\
1 & -1 & 0 & 0 & 0 \\
0 & 1 & 1 & 0 & -1 \\
0 & 0 & 0 & 1 & 1 \\
\end{bmatrix}\begin{bmatrix}
y_1\\
y_2\\
y_3\\
y_4\\
y_5\\
\end{bmatrix}=\begin{bmatrix}
0 \\
0 \\
0 \\
0 \\
\end{bmatrix}
\] 变为简化行阶梯\(R\)就会发现:pivot
col是第一列、第二列和第四列,对应到图中的三条边,可以看到是没有环路的,实际上是一棵最小生成树。如果用\(y_i\)表示边\(i\)的电流值,不妨写出这个方程组:
\[
\begin{cases}
-y_1-y_3-y_4=0& \text{结点1流出之和为0}\\
y_1-y_2=0& \text{结点2流入流出相等}\\
y_2+y_3-y_5=0& \text{...}\\
y_4+y_5=0& \text{...}
\end{cases}\] 类似地,可以求出这个左零空间的一组基: \[
\begin{bmatrix}
1\\
1\\
-1\\
0\\
0\\
\end{bmatrix}、\begin{bmatrix}
0\\
0\\
1\\
-1\\
1\\
\end{bmatrix}
\]
这组基对应到图中也是很明确的:第一个向量对应回路1(边1/2/3)的电流,第二个向量对应回路2(边3/4/5)的电流,当然也可以选择大的回路作为基的一个组成。
由此也可以看出:\(dim(N(A^T))=m-r=\#loops=\#edges-(\#nodes-1)\),这也就是著名的欧拉公式:\(\#nodes-\#edges+\#loops=1\)。
回顾整个过程:
- 通过电势求得电势差:\(Ax=e\);
- 通过欧姆定律\(y=Ce\)可以求得结点间的电流值\(y_i\);
- 通过\(A^Ty=0\)验证了Kirchhoff's current law。
如果有外接电流源,那么整个过程可以描述为\(A^TCAx=f\)。
马尔可夫矩阵
马尔可夫模型最初是研究人口迁徙的模型,马尔可夫矩阵有2个特点: - \(a_{ij}>0\) - 每一列和为1
我们要研究随着时间变化,人口最终的分布情况,即稳态。
根据一阶差分\(u_k=A^ku_0=c_1\lambda_1^kx_1+c_2\lambda_2^kx_2+...\),马尔可夫矩阵有一个特征值为1,其余的绝对值都小于1,那么最终的稳态就是\(c_1x_1\)。
举例来看: \[
\begin{bmatrix}
u_{cal}\\
u_{mass}\\
\end{bmatrix}_{t=k+1}=\begin{bmatrix}
0.9 & 0.2\\
0.1 & 0.8\\
\end{bmatrix}\begin{bmatrix}
u_{cal}\\
u_{mass}\\
\end{bmatrix}_{t=k},u_0=\begin{bmatrix}
0\\
1000\\
\end{bmatrix}
\] 矩阵表示加州的人有0.9留在加州,0.1迁徙到麻省。求得\(A\)的特征值和特征向量,再用\(u_0\)求得系数\(c\),就可以得到\(u_k\)。
傅里叶级数
我们知道,向量空间内任意向量都可以表示为一组标准正交基的线性组合: \[ v=x_1q_1+x_2q_2+...+x_nq_n=Qx,x=Q^{-1}v=Q^Tv \] 那么对于任意的函数\(f(x)\),也可以表示为一组正交基的线性组合: \[ f(x)=a_0*1+a_1cosx+b_1sinx+a_2cos(2x)+b_2sin(2x)+... \] 这组基\(1,cosx,sinx,cos(2x),sin(2x),...\)是正交的,即: \[ f^Tg=\int_0^{2\pi} f(x)g(x) dx=0 \] 要求得级数得系数,比如\(a_1\),只要等式两边同乘\(cosx\)并积分即可: \[ \int_0^{2\pi} f(x)cosx dx=\int_0^{2\pi} a_1cos^2(x) dx \]
复矩阵
复向量\(Z=\begin{bmatrix}
z_1\\
...\\
z_n\\
\end{bmatrix}\)的模\(||Z||^2=\bar
Z^TZ=||z_1||^2+...+||z_n||^2\),内积也变为共轭转置\(\bar y^Tx\)。
复数意义下的对称是\(\bar
A^T=A\),也叫Hermitian矩阵;
复数意义下的正交是\(\bar
q_i^Tq_j=\begin{cases}
0,i\neq j\\
1,i=j\\
\end{cases}\),这样组成的正交阵\(\bar
Q^TQ=I\),\(Q\)也叫unitary矩阵。

