正交向量
初中时候我们学过勾股定理,现在用向量的形式表示: \[ |x|^2+|y|^2=|x+y|^2 \] 模长的平方也可以表示为\(x^Tx\),做一些计算,就有两个向量正交的判断条件\(x^Ty=0\)。
向量正交有些简单,让我们上升到子空间正交。一个比较直观的错误的例子就是地板和墙壁的关系,两者并不正交,因为子空间正交要求子空间\(S\)中的每个向量都和子空间\(T\)中每个向量正交。根据定义,任意两个子空间若相交于某非0向量,那么两者必然不正交。
将正交的概念应用于前面学过的四个基本子空间:
对于零空间\(Ax=0\),我们有\(\begin{bmatrix}
row1\\
...\\
rowm
\end{bmatrix}x=\begin{bmatrix}
0\\
...\\
0
\end{bmatrix}\),\(x\)和每一行都是正交的,那么\(x\)和各行的线性组合也正交,由此可见零空间和行空间是正交的。
我们还知道:在\(R^n\)中,需要\(n\)个基向量张成整个空间,\(dim(C(A^T))=r,dim(N(A))=n-r\),这两个正交的子空间将\(R^n\)一分为二,有个专门的术语正交补就描述了这种关系,意即零空间包含了所有垂直于行空间的向量。
类似地,可以证明\(C(A)\)和\(N(A^T)\)也是正交补的关系,将\(R^m\)一分为二。
最后,我们为下一节留一个引子:考虑\(Ax=b\),当方程个数\(m\)大于未知数个数\(n\),方程组很可能无解,那么怎么找到一个最为近似的解呢?听起来可能有些难理解,举个例子来看:
\[
\begin{bmatrix}
1 & 1\\
1 & 2\\
1 & 5\\
\end{bmatrix}\begin{bmatrix}
x_1\\
x_2\\
\end{bmatrix}=\begin{bmatrix}
b_1\\
b_2\\
b_3\\
\end{bmatrix}
\] \(A\)的列空间是\(R^3\)中的一个平面,但是向量\(b\)极有可能不在列空间中,此时方程组无解。但是我们想找到\(b\)在列空间的投影,进而求出最为近似的解。
做法是在\(Ax=b\)两边同乘\(A^T\),求解\(A^TA\hat x=A^Tb\),\(\hat
x\)即是要求的近似解。这里牵涉到一个非常重要的矩阵\(A^TA\),它是对称阵,并且\(N(A^TA)=N(A),r(A^TA)=r(A)\),如果\(A\)的各列线性无关,那么\(A^TA\)就是可逆的。这样做的原因后面会逐渐揭晓。
子空间投影
这一节非常重要。上一节的最后我们说到:在\(Ax=b\)无解的情况下,我们要将\(b\)微调成最靠近\(C(A)\)的某个向量\(p\),从而求解\(A\hat x=p\),\(p\)就是\(b\)在列空间的投影。
我们首先看看\(R^2\)的情况:

从图中可以看到:\(e=b-p=b-xa\),再由正交关系:\(a^Te=a^T(b-xa)=0\),可以计算出乘数\(x=\frac{a^Tb}{a^Ta}\),进而可以将投影\(p\)表示为\(p=xa=\frac{aa^T}{a^Ta}b=Pb\),这里的\(P=\frac{aa^T}{a^Ta}\)即投影矩阵。
\(r(P)=1\),\(P\)的列空间即为过\(a\)的直线。此外,投影矩阵还有两条性质:\(P^T=P,P^2=P\),从几何上解释即投影2次和投影1次效果完全一样。
接着看看\(R^3\)的情况:
两个线性无关的列向量\(a_1,a_2\)生成的列空间是一个平面,令\(A=\begin{bmatrix}
a_1 & a_2\\
\end{bmatrix}\)。类似地,\(p\)是向量\(b\)在平面上的投影,\(e=b-p\)垂直于平面。因为\(p\)在\(A\)的列空间中,所以可以表示为\(p=A\hat x=\hat x_1a_1+\hat
x_2a_2\),我们就是要找到\(\hat
x\)。
根据\(e\)和平面的垂直关系,可以得到: \[
\begin{cases}
a_1^T(b-A\hat x)=0& \text{}\\
a_2^T(b-A\hat x)=0& \text{}
\end{cases}\] 写出矩阵形式: \[
\begin{bmatrix}
a_1^T\\
a_2^T\\
\end{bmatrix}\begin{bmatrix}
b-A\hat x \\
\end{bmatrix}=\begin{bmatrix}
0\\
0\\
\end{bmatrix}
\] 即\(A^T(b-A\hat
x)=0\),这里\(b-A\hat
x=e\)在\(N(A^T)\)中,故\(e\)垂直于\(C(A)\)。
接着化简,我们得到了上一节中同乘\(A^T\)的原因:\(A^TA\hat x=A^Tb\),继续:\(\hat
x=(A^TA)^{-1}A^Tb\)。这里注意不能继续化简,因为\(A\)不是方阵,\(A^{-1}\)不存在。
得到组合系数\(\hat
x\)后,就可以写出投影\(p=A\hat
x=A(A^TA)^{-1}A^Tb\),同样地,投影矩阵\(P=A(A^TA)^{-1}A^T\),可以验证,\(P^T=P,P^2=P\)仍然成立。
最后我们考虑极端一些的情况:
- 若\(b\)在\(A\)的列空间中,投影后仍然是\(b\)自己:\(b=Ax->Pb=PAx=Ax=b\);
- 若\(b\)垂直于\(A\)的列空间,投影后是\(0\):\(b\)在\(N(A^T)\)中,\(A^Tb=0->Pb=0\)。
换句话说,\(b\)被分解为\(p\)和\(e\),\(p\)在\(C(A)\)中,\(e\)在\(N(A^T)\)中,并且\(b=p+e=Pb+(I-P)b\)。
最小二乘法
这是投影的一个应用,主要用来拟合直线,举例来看:
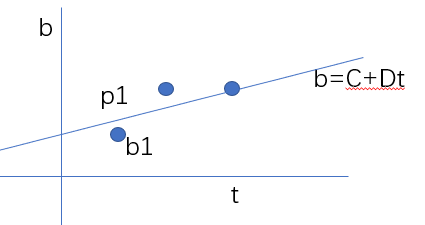
有三个点,需要找到一条最佳拟合直线,方程组形式: \[
\begin{cases}
C+D=1& \text{}\\
C+2D=2& \text{}\\
C+3D=2& \text{}\\
\end{cases}\] 矩阵形式: \[
Ax=\begin{bmatrix}
1 & 1\\
1 & 2\\
1 & 3\\
\end{bmatrix}\begin{bmatrix}
C\\
D\\
\end{bmatrix}=\begin{bmatrix}
1\\
2\\
2\\
\end{bmatrix}=b
\] 显然是无解的,要找到最优拟合系数\(CD\),就要用到投影:
清除outlier(离群值)后,定义每个点的误差:\(|e|^2=|Ax-b|^2\),那么优化目标变为最小化:\(e_1^2+e_2^2+e_3^2=(C+D-1)^2+(C+2D-2)^2+(C+3D-2)^2\),如何找到\(\hat x=\begin{bmatrix}
C\\
D\\
\end{bmatrix}\)?
求偏导当然是一种方法,从线性代数的角度,回顾下上节中\(A^TA\hat
x=A^Tb\),我们已经证明,这样解得的\(\hat x\)可以微调\(b\)使其最靠近\(C(A)\),也就是我们要的最优估计。
所以我们有: \[
A^TA\hat x=\begin{bmatrix}
3 & 6\\
6 & 14\\
\end{bmatrix}\begin{bmatrix}
C\\
D\\
\end{bmatrix}=\begin{bmatrix}
5\\
11\\
\end{bmatrix}=A^Tb
\] 这样就得到了所谓的Normal Equation: \[
\begin{cases}
3C+6D=5& \text{}\\
6C+14D=11& \text{}\\
\end{cases}\] 解得\(C=\frac{2}{3},D=\frac{1}{2}\),我们的最佳拟合直线即为\(b=\frac{2}{3}+\frac{1}{2}t\)。
最后要注意的一点:\(\hat
x\)可解的前提是\(A^TA\)可逆,只要\(A\)的各列线性无关,这点即可满足。
不妨做一些证明:
要证明\(A^TA\)可逆即证明\(A^TAx=0\)只有零解;
\(x^TA^TAx=0,(Ax)^TAx=0,Ax=0\),\(A\)的各列线性无关意即\(Ax=0\)只有零解,得证。
正交化
我们都知道,对于标准正交向量,有: \[
q_i^Tq_j=\begin{cases}
0& \text{$i\neq j$}\\
1& \text{$i=j$}\\
\end{cases}
\] 正交矩阵写作\(Q=\begin{bmatrix}
q_1 & q_2 ... & q_n\\
\end{bmatrix}\),很容易验证: \[
Q^TQ=\begin{bmatrix}
q_1^T\\
...\\
q_n^T\\
\end{bmatrix}\begin{bmatrix}
q_1 & ... & q_n\\
\end{bmatrix}=I
\] 如果\(Q\)是方阵,那么\(Q^T=Q^{-1}\)。正交矩阵的例子有很多:以前学习过的置换矩阵、\(\begin{bmatrix}
cos\theta & -sin\theta\\
sin\theta & cos\theta\\
\end{bmatrix}\),还有一种叫做Adhemar的系列矩阵也是正交阵:\(\frac{1}{\sqrt{2}}\begin{bmatrix}
1 & 1\\
1 & -1\\
\end{bmatrix}\)、\(\frac{1}{2}\begin{bmatrix}
1 & 1 & 1 & 1\\
1 & -1 & 1 & -1\\
1 & 1 & -1 & -1\\
1 & -1 & -1 & 1\\
\end{bmatrix}\)...
有了这些了解后,就可以解答为什么需要正交矩阵:
还记得上一节中的投影矩阵\(P\)吗?将矩阵\(A\)变为正交阵\(Q\)后,这时再把\(b\)投影到\(C(Q)\)中,投影矩阵就变为了\(P=Q(Q^TQ)^{-1}Q^T=QQ^T\),如果\(Q\)是方阵,那么\(P=QQ^T=I\),这也非常好解释:\(Q\)是方阵必然可逆,\(C(Q)\)就是整个空间,\(P=I\)相当于没有进行投影。
还有我们在求最优估计时用到的\(A^TA\hat
x=A^Tb\)变为了\(Q^TQ\hat
x=Q^Tb\),即\(\hat
x=Q^Tb\),求解\(\hat
x_i\)就简化为了\(\hat
x_i=q_i^Tb\)。
所以接下来的问题就是如何将各列线性无关的\(A\)变为正交阵\(Q\),这项工作就是Gram-Schmidt正交化,先从两个向量的情况开始:
工作分2步进行:
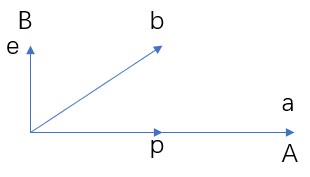
- 由线性无关的2个向量\(a,b\)得到2个正交的向量\(A,B\): 这一步主要是改变方向,\(A=a\)即可,\(B=e=b-p=b-\frac{A^Tb}{A^TA}A\)。
- 将\(A,B\)变为标准正交向量\(q_1,q_2\): 这一步主要是改变长度,\(q_1=\frac{A}{|A|},q_2=\frac{B}{|B|}\)。
如果是3个线性无关的向量,必然生成整个三维空间,\(A,B\)不会变,\(C\)其实是垂直于\(AB\)子空间的那个\(e\),即减去在\(A,B\)两个方向的投影(可以用三支笔模拟),故\(C=c-\frac{A^Tc}{A^TA}A-\frac{B^Tc}{B^TB}B\)。
观察上述工作,可以发现:我们所有的工作都是在同一个列空间中进行,只是开始的线性无关的基计算量太大,我们想要一组更加简化计算的互相垂直且长度为1的基。
正因为是在一个空间中进行,所以必然存在\(q\)的线性组合可以得到\(a\),即\(A=QR\),并且\(a_1\)只与\(q_1\)有关、\(a_2\)只与\(q_1,q_2\)有关、\(a_3\)只与\(q_1,q_2,q_3\)有关,故\(R\)必为上三角矩阵,也即:
\[
\begin{bmatrix}
a_1 & a_2 & a_3\\
\end{bmatrix}=\begin{bmatrix}
q_1 & q_2 & q_3\\
\end{bmatrix}\begin{bmatrix}
q_1^Ta_1 & q_1^Ta_2 & q_1^Ta_3\\
0 & q_2^Ta_2 & q_2^Ta_3\\
0 & 0 & q_3^Ta_3\\
\end{bmatrix}
\] 这里\(R=Q^TA\)。
作业
Suppose a square \(A\) has an LU
factorization \(A=LU\) where \(L\) and \(U\) are invertible. If \(A=QR\), what is \(r_{11}\) in terms of possibly elements of
\(L\) and \(U\)?
在QR分解中,\(r_{11}=q_1^Ta_1=\frac{a_1}{||a_1||}a_1=||a_1||\),即\(A\)第一列的模;第一列即\(L\)各列的线性组合,系数是\(U\)的第一列(只有\(U_{11}\)一个元素),所以\(r_{11}=U_{11} \sqrt{\sum_i
L_{i1}^2}\)。

