Knapsack Problem

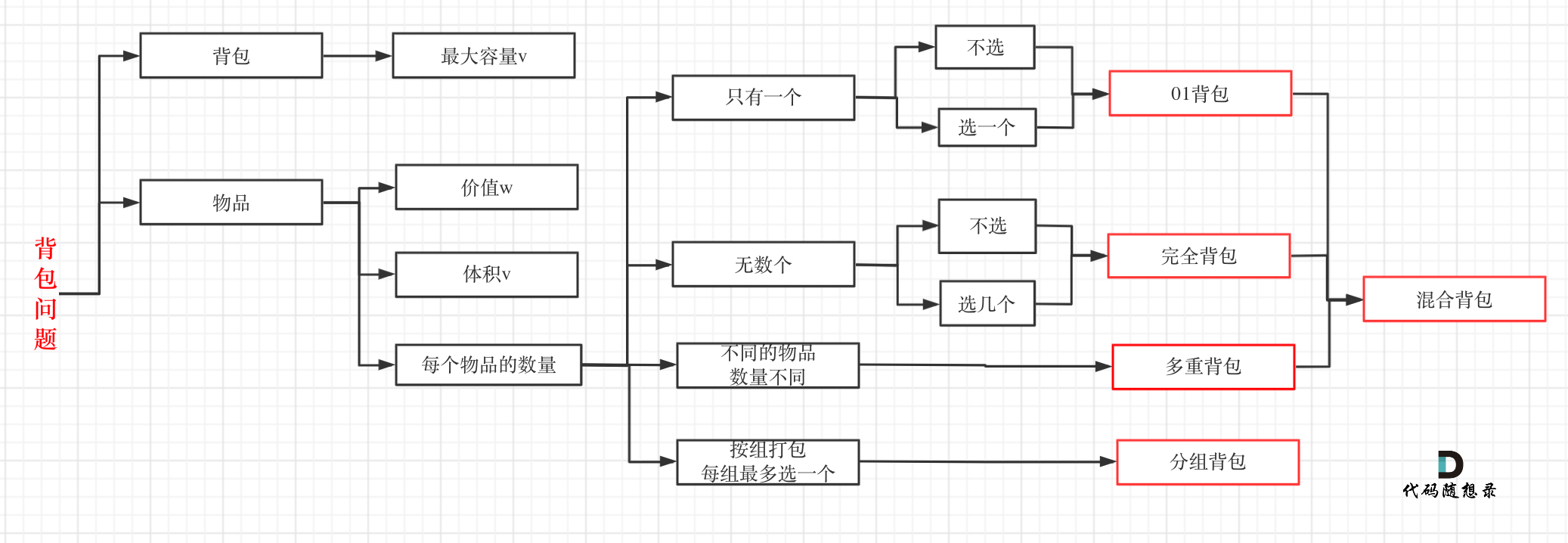
0-1背包

描述：N件物品，第i件的重量是w[i]，价值v[i]。有一个容量为W的背包，求将哪些物品放入背包可使总价值最大。每件物品可以用0或1次。
分析：根据题意，可以写出表达式： \[max(\Sigma v_ix_i), s.t. \Sigma w_ix_i<=W, x_i\in\{0, 1\}\] 最直接的思路就是：对于每件物品，都有yes/no两种选择，尝试所有的组合，记录每个组合的价值，选出满足重量条件的最大价值。时间复杂度\(O(2^n)\)，空间复杂度\(O(n)\)。

// backtracking
class knapsack01 {
public:
    int knapsack(int W, vector<int>& w, vector<int>& v, string& ans) {
        string cur(w.size(), '0');

        dfs(0, 0, 0, W, w, v, cur, ans);
        return maxV;
    }
private:
    void dfs(int s, int curW, int curV, int W, vector<int>& w, vector<int>& v, string& cur, string& ans) {
        // 到达叶子结点，得到一个解，所以在这里更改最终结果
        if (s >= w.size()) {
            if (maxV < curV) {
                ans.assign(cur);
                maxV = curV;
            }
            return;
        }

        // as for goods s, two choices
        for (int i = 0; i < 2; ++i) {
            cur[s] = i + '0';

            if (curW + i * w[s] <= W) {
                curW += i * w[s];
                curV += i * v[s];
                dfs(s + 1, curW, curV, W, w, v, cur, ans);
                curW -= i * w[s];
                curV -= i * v[s];
            }
        }
    }

    int maxV = 0;
};

上面的程序可以通过剪枝进行优化，下来换一种思路：
令dp[i][j]表示有前i件物品可选，背包容量为j时具有的最大价值，问题转化为求dp[N][0...W]的最大值，边界条件：

// 第一列全0，第一行取决于物品0体积与背包大小关系
vector<vector<int>> dp(w.size(), vector<int>(W + 1, 0));
for (int j = w[0]; j <= W; ++j) {
    dp[0][j] = v[0];
}

假设3件物品，\(w=\{1,1,2\}\)，\(v=\{1,2,4\}\)，\(W=2\)，先用递归形式分析，每件物品只有yes/no两种状态：

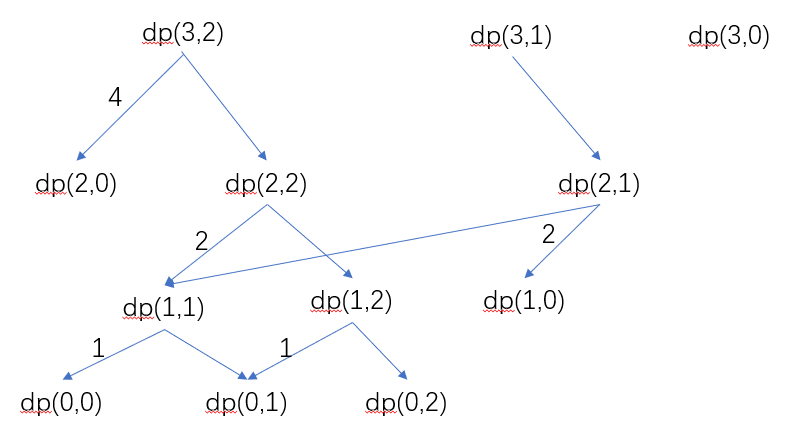可以看到，求解过程中有很多重叠子问题，故可以采用记忆化递归求解，时间复杂度即为子问题数量\(O(NW)\)，空间复杂度\(O(NW)\)。
记忆化递归可以写成自底向上的动态规划，状态转移方程： \[dp[i][j]=max\{dp[i-1][j], v[i]+dp[i-1][j-w[i]]\}\]

// dp->space complexity O(NW)
class knapsack01 {
public:
    int knapsack(int W, vector<int>& w, vector<int>& v) {
        const int N = w.size();
        vector<vector<int>> dp(N + 1, vector<int>(W + 1, 0));
        for (int i = 1; i <= N; ++i)
            for (int j = 1; j <= W; ++j) {
                if (j < w[i - 1]) {
                    dp[i][j] = dp[i - 1][j];
                }
                else {
                    dp[i][j] = max(dp[i - 1][j], v[i - 1] + dp[i - 1][j - w[i - 1]]);
                }
            }
        return dp[N][W];
    }
};

前i件物品只依赖于前i-1件物品，\(dp\)数组的更新方向为：

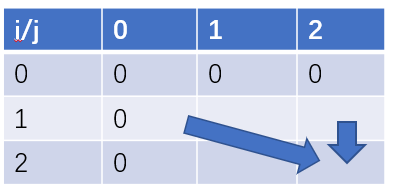
所以可以使用滚动数组降低空间复杂度为\(O(W)\)：

// dp->space complexity O(W)
class knapsack01 {
public:
    int knapsack(int W, vector<int>& w, vector<int>& v) {
        const int N = w.size();
        vector<int> dp(W + 1, 0);
        for (int i = 1; i <= N; ++i) {
            // iterate j reversely, avoid dp override
            for (int j = W; j >= w[i - 1]; --j) {
                dp[j] = max(dp[j], v[i - 1] + dp[j - w[i - 1]]);
            }
        }
        return dp[W];
    }
};

01背包有一些细节需要注意：

两个for循环的先后：核心在于当前值取决于其正上方的值和上一行前面的某个值，二维中行优先和列优先都可以保证更新当前值之前其需要的两个值已经更新，故可以颠倒；一维中列优先是不可以的，因为上一行前面的某个值会被覆盖
二维和一维j的遍历顺序：二维正反都可以；一维只能反向，否则会被覆盖

有一道比较类似的题目Target Sum，分析下此题顺便再练习下DP的套路。
题意是这样：给定一些非负数字，可以给每个数字添上+或-号，使得添加后的所有数字之和等于S。数组大小不超过20，S大小不超过1000。
我第一次做感觉这是个纯暴力DFS，枚举所有可能，复杂度\(O(2^n)\)。这道题和0/1背包不同之处在于：数组里的所有数字都必须用到。

接着我们试着做一些优化：
换种方式看问题：在这堆数字中选一些作为正数集合\(P\)，剩下作为负数集合\(N\)，那么有\(sum(P)-sum(N)=S\)，\(sum(P)+sum(N)+sum(P)-sum(N)=sum(nums)+S=2*sum(P)\)，故\(sum(P)=(sum(nums)+S)/2\)，同时注意到\(sum(nums)+S\)是偶数。
所以问题转化为在数组中寻找一些数作为正数，使得这些数的和为\((sum(nums)+S)/2\)，求这样的组合有多少种。这就转化为了0/1背包问题。

我们用\(dp(i,j)\)表示从前i个数中选出和为j的方案数目，有状态转移方程\(dp(i,j)=dp(i-1,j)+dp(i-1,j-nums[i])\)，如果纯粹暴力递归，有很多重叠子问题（类似背包问题的那个图）。Base Case就是，\(dp(0,0)=1\)，即选出和为0的方案，就是每个都不选一种；否则当i = 0 || j < 0时，\(dp(i,j)=0\)。

所以先用记忆化搜索：

class Solution {
public:
    int findTargetSumWays(vector<int>& nums, int S) {
        int sum = 0;
        for (int num : nums)
            sum += num;
        vector<vector<int>> memo(21, vector<int>(1001, -1));
        return sum < S || (sum + S) & 1 ? 0 : cnt(nums, memo, nums.size(), (sum + S) >> 1);
    }
private:
    int cnt(vector<int>& nums, vector<vector<int>>&memo, int idx, int sum) {
        if (!idx && !sum)
            return 1;
        if (!idx || sum < 0)
            return 0;
        
        if (memo[idx][sum] > 0)
            return memo[idx][sum];
        memo[idx][sum] = cnt(nums, memo, idx - 1, sum) + cnt(nums, memo, idx - 1, sum - nums[idx - 1]);
        return memo[idx][sum];
    }
};

改一下Bottom-Up的形式，更新方向从左到右、从上到下，注意这里j不能从nums[i - 1]开始，否则j的前半部分无法更新到正确的值，后面如果用到就是错误的值。

class Solution {
public:
    int findTargetSumWays(vector<int>& nums, int S) {
        int sum = 0;
        for (int num : nums)
            sum += num;
        if (sum < S || (sum + S) & 1)
            return 0;
        
        vector<vector<int>> dp(21, vector<int>(1001, 0));
        dp[0][0] = 1;
        for (int i = 1; i <= nums.size(); ++i) {
        	// 不能for (int j = nums[i - 1]; j <= (sum + S) >> 1; ++j)
            for (int j = 0; j <= (sum + S) >> 1; ++j) {
                dp[i][j] = dp[i - 1][j];
                if (j >= nums[i - 1]) {
                    dp[i][j] += dp[i - 1][j - nums[i - 1]];
                }
            }
        }
        return dp[nums.size()][(sum + S) >> 1];
    }
};

最后来优化空间：\(dp(i,j)\)取决于\(dp(i-1,j)\)和\(dp(i-1,j-num[i-1])\)，所以只要用一个一维数组\(dp(j)\)记录上一行的所有值即可，这里必须反向更新，因为如果正向，上一行的j-num[i-1]位置已经被新值覆盖，计算结果出错。如果反向：上一行需要的2个位置都没有被覆盖：\(dp(j)=dp(j)+dp(j-nums[i-1])\)。
初始时候(0,0)位置为1，即\(dp(0)=1\)，以后\(dp(0)\)会不断更新。

class Solution {
public:
    int findTargetSumWays(vector<int>& nums, int S) {
        int sum = 0;
        for (int num : nums) {
            sum += num;
        }
        return sum < S || (S + sum) & 1 ? 0 : numSubsetSum(nums, (S + sum) >> 1);
    }
private:
    int numSubsetSum(vector<int>& nums, int target) {
        vector<int> dp(target + 1, 0);
        dp[0] = 1;
        for (int i = 0; i < nums.size(); ++i) {
            /* 等价写法
        	for (int j = target; j >= 0; --j){
					if (j - nums[i] >= 0)
						dp[j] += dp[j - nums[i]];
			} */
            // 只有j>=nums[i]才更新，否则沿用上一行的值
            for (int j = target; j >= nums[i]; --j) {
                dp[j] += dp[j - nums[i]];
            }
        }
        return dp[target];
    }
};

完全背包

每件物品可以使用任意多次。
一个Naive的思路：虽然题目描述每件物品可以使用任意多次，但实际上由于W的限制，每件物品最多使用\(\lfloor W/w[i] \rfloor\)次。这样我们可以将每件物品拆为\(\lfloor W/w[i] \rfloor\)件，问题就转化为了0-1背包。子问题仍然有NW个，但是求解每个子问题需要\(O(W/w[i])\)，总的时间复杂度\(O(\Sigma (W/w[i])*W)\)，也即\(O(W*拆后物品件数)\)。
更tricky的做法：W无法改变，只能改变拆后物品件数。这里可以使用二进制的思想：假设我们某件物品可以使用\(10=8+2\)次，原本需要复制出10件，现在只要复制出2件，价值和重量是原来的8倍和2倍，这样就降低了复杂度。
完全背包有\(O(NW)\)的算法

\(dp(i,j)=max\{dp(i-1,j-kw[i])+kv[i]\},0\leq kw[i]\leq j\)
为了得到更加简洁的表示，考虑： \[ dp(i,j-w[i])=max\{dp(i-1,j-w[i]-aw[i])+av[i]\},0\leq aw[i]\leq j-w[i],a\geq 0 \\ =max\{dp(i-1,j-(a+1)w[i])+av[i]\},0\leq aw[i]\leq j-w[i],a\geq 0 \\ =max\{dp(i-1,j-kw[i])+(k-1)v[i]\},0\leq (k-1)w[i]\leq j-w[i],k\geq 1 \\ =max\{dp(i-1,j-kw[i])+kv[i]\}-v[i],0\leq (k-1)w[i]\leq j-w[i],k\geq 1 \] 因此当\(k\geq 1\)时有\(max\{dp(i-1,j-kw[i])+kv[i]\}=dp(i,j-w[i])+v[i]\)
综上有\(dp(i,j)=max\{dp(i-1,j),dp(i,j-w[i])+v[i]\}\)，状态\(dp(i,j-w[i])\)包含了第i件物品被选择若干次后的最大价值。

int knapsackUnbounded(int W, vector<int>& w, vector<int>& v) {
    const int N = w.size();
    vector<vector<int>> dp(N + 1, vector<int>(W + 1, 0));
    for (int i = 1; i <= N; ++i) {
        for (int j = 1; j <= W; ++j) {
            if (j < w[i - 1]) {
                dp[i][j] = dp[i - 1][j];
            }
            else {
                dp[i][j] = max(dp[i - 1][j], v[i - 1] + dp[i][j - w[i - 1]]);
            }
        }
    }
    return dp[N][W];
}

int knapsackUnbounded(int W, vector<int>& w, vector<int>& v) {
    const int N = w.size();
    vector<int> dp(W + 1, 0);
    for (int i = 1; i <= N; ++i) {
        for (int j = w[i - 1]; j <= W; ++j) {
            dp[j] = max(dp[j], v[i - 1] + dp[j - w[i - 1]]);
        }
    }
    return dp[W];
}

完全背包两个for循环的顺序也可以颠倒，但是j的遍历只能而且应该正向。

多重背包

每件物品最多可以使用\(num[i]\)次。
同样，Naive的思路就是将每件物品都复制\(num[i]\)次，问题转化为0-1背包，复杂度\(O(\Sigma nums[i]*W)\)。
将\(num[i]\)用二进制表示，价值和重量变为原来的相应倍，降低复杂度。

Future

后续还有混合背包、二维费用的背包等，详情可以学习背包九讲。