Stanford的帅哥Jure发在NIPS 2017的一篇文章。
GCN是Transductive Learning,训练时的图要包含所有结点,是固定的,不能快速泛化到未知结点(图),本文提出了一种Inductive Learning的GraphSAGE。
GCN学习的是每个单独节点的低维embedding,由于输入的图是固定的,所以可以很好捕获全局信息。但如果要获得新节点的embedding,加入图以后需要调整其它结点,至少也是局部重新训练,计算开销太大,应用受限。
GraphSAGE学习的不是每个结点的固定的表示,因为图结构不断变化,所以学习一种节点表示的函数,这样就可以快速得到未知结点的表示。
简单来说:学习每个结点的特征如何由邻居的特征聚合而来,学到聚合函数后,只要已知新节点的特征和邻边关系,就能得到表示,并且这个表示会由于图结构的变化而变化,是动态的。
前向传播是为了生成结点的向量表示,

如果聚合K次,就需要K个聚合函数,初始时每个结点的表示是原本的特征向量,对第k层,对结点v,先得到v的第k层结点的聚合表示,加上v在上一层的特征,最后得到v的最终表示。
以作者的图为例,
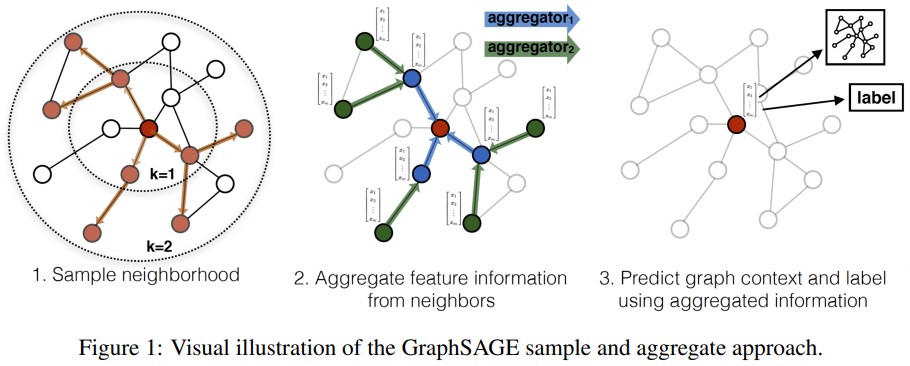
我觉得知乎上这张更清楚: 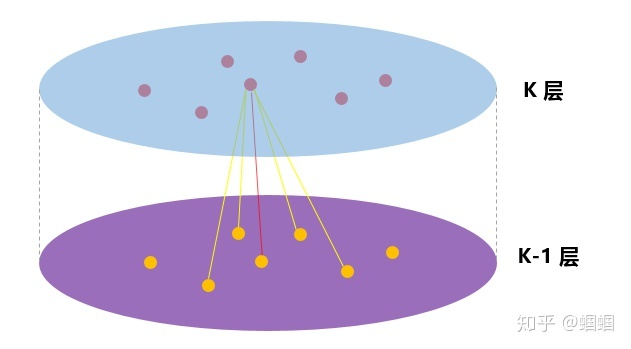
每一层的表示都是由上一层生成,与当前层其他节点无关。
由于需要学习参数,所以要设计损失函数。无监督学习的损失函数应该是让临近节点有相似的表示,有监督学习用cross-entropy即可。
聚合函数作者给了3种选择:
- Mean
取邻居的平均值 - LSTM
- Pooling

