Gradient Boosting

Gradient Boosting Regression

Gradient Boosting Classification

XGBoost

决策树集成

集成学习可以组合多个基学习器，产生更加优异的性能。将决策树（如CART）作为基学习器，结合每个基学习器的预测结果作为最终输出，就像下图这样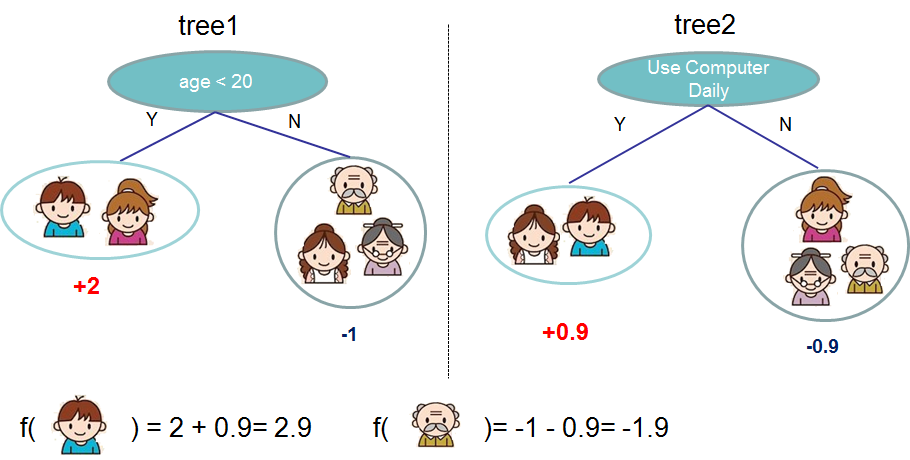：正式一些的表示： \[\hat{y}_i = \sum_{k=1}^K f_k(x_i), f_k \in \mathcal{F}\] 其中，\(K\)是决策树个数，\(f_k(x_i)\)表示第\(k\)个决策树的预测值。

为了定量描述模型参数与训练数据的匹配程度，我们还要定义待优化的目标函数： \[\text{obj}(\theta) = \sum_i^n l(y_i, \hat{y}_i) + \sum_{k=1}^K \Omega(f_k)\] ## Boosting Decision Tree 集成多棵树的方式可以是Bagging，也可以是Boosting。Boosting的motivation是用一棵新树不断拟合当前的集成模型与真实值的残差，拟合后将该树也加入模型中，即所谓的Additive Training： \[\hat{y}_i^{(0)} = 0\\ \hat{y}_i^{(1)} = f_1(x_i) = \hat{y}_i^{(0)} + f_1(x_i)\\ \hat{y}_i^{(2)} = f_1(x_i) + f_2(x_i)= \hat{y}_i^{(1)} + f_2(x_i)\\ \dots\\ \hat{y}_i^{(t)} = \sum_{k=1}^t f_k(x_i)= \hat{y}_i^{(t-1)} + f_t(x_i)\] 好了，接下来的问题就是每次迭代时的那棵新树\(f_t\)要怎么训练呢？一个直观的想法就是选择那棵令目标函数最小的树： \[\text{obj}^{(t)} = \sum_{i=1}^n l(y_i, \hat{y}_i^{(t)}) + \sum_{i=1}^t\Omega(f_i) \\ = \sum_{i=1}^n l(y_i, \hat{y}_i^{(t-1)} + f_t(x_i)) + \Omega(f_t) + \mathrm{constant}\] 我们先选择MSE作为损失函数，看看会发生什么： \[{obj}^{(t)} = \sum_{i=1}^n (y_i - (\hat{y}_i^{(t-1)} + f_t(x_i)))^2 + \sum_{i=1}^t\Omega(f_i) \\ = \sum_{i=1}^n [2(\hat{y}_i^{(t-1)} - y_i)f_t(x_i) + f_t(x_i)^2] + \Omega(f_t) + \mathrm{constant}\] 虽然MSE的形式比较友好，但是如果选择其它损失函数就很难有上式那般人性了，吃得太饱的同学可以试试logistic loss： \[L(\theta) = \sum_i[ y_i\ln (1+e^{-\hat{y}_i}) + (1-y_i)\ln (1+e^{\hat{y}_i})]\] 为了增强可扩展性、便于计算，一般采用损失函数的二阶泰勒展开去做一个近似： \[\text{obj}^{(t)} = \sum_{i=1}^n [l(y_i, \hat{y}_i^{(t-1)}) + g_i f_t(x_i) + \frac{1}{2} h_i f_t^2(x_i)] + \Omega(f_t) + \mathrm{constant}\] 其中，\(g_i = \partial_{\hat{y}_i^{(t-1)}} l(y_i, \hat{y}_i^{(t-1)}),h_i = \partial_{\hat{y}_i^{(t-1)}}^2 l(y_i, \hat{y}_i^{(t-1)})\)。扔掉所有常数项，就得到了第\(t\)步的目标函数： \[\sum_{i=1}^n [g_i f_t(x_i) + \frac{1}{2} h_i f_t^2(x_i)] + \Omega(f_t)\]

弄完了training loss，接着还得研究下正则项\(\Omega(f_t)\)，首先得给\(f(x)\)来一个正式点的定义： \[f_t(x) = w_{q(x)}, w \in R^T, q:R^d\rightarrow \{1,2,\cdots,T\} .\] 其中，\(w\)是叶子结点的得分向量，\(q\)是将样本点映射到对应叶子的函数，\(T\)是叶子数目。如果有点抽象，就看看上图中的左子图吧：\(w=[2,-1],f(男孩)=w_{q(男孩)}=w_0=2\)。

模型复杂度的具体定义随你了，XGBoost是这么定义的： \[\Omega(f) = \gamma T + \frac{1}{2}\lambda \sum_{j=1}^T w_j^2\] 就用上式重新写出我们第\(t\)步的目标函数： \[\text{obj}^{(t)} \approx \sum_{i=1}^n [g_i w_{q(x_i)} + \frac{1}{2} h_i w_{q(x_i)}^2] + \gamma T + \frac{1}{2}\lambda \sum_{j=1}^T w_j^2\\ = \sum^T_{j=1} [(\sum_{i\in I_j} g_i) w_j + \frac{1}{2} (\sum_{i\in I_j} h_i + \lambda) w_j^2 ] + \gamma T\] 其中，\(I_j = \{i|q(x_i)=j\}\)表示第\(j\)个叶子中样本点的索引集合，由于任意一个叶子中样本点得分相同，因此上式写成了对\(T\)个叶子的求和。

令\(G_j = \sum_{i\in I_j} g_i\)及\(H_j = \sum_{i\in I_j} h_i\)，就有了一个相对简洁的表示： \[\text{obj}^{(t)} = \sum^T_{j=1} [G_jw_j + \frac{1}{2} (H_j+\lambda) w_j^2] +\gamma T\] 因为叶子之间相互独立，所以令目标函数最优的得分向量\(w\)为： \[w_j^\ast = -\frac{G_j}{H_j+\lambda}\\ \text{obj}^\ast = -\frac{1}{2} \sum_{j=1}^T \frac{G_j^2}{H_j+\lambda} + \gamma T\] 目标函数\(obj^*\)的值衡量着本次迭代树结构\(q(x)\)对训练数据的拟合程度。

云里雾里一大堆，我都烦了，来看个例子：假设在第\(t\)次迭代选了这么一棵树，按照if-then规则将训练样本分到相应的叶子，将梯度信息相加得到每个叶子对应的\(G,H\)，接着用\(obj^*\)计算这棵树最小的损失，不行就换一种树结构，以求减小\(obj^*\)。

忙活了大半天，终于知道了怎么度量一棵树的好坏。那么只要枚举所有可能的树结构，选那个令\(obj^*\)最小的就好了。傻子都知道这是不行滴，所以只能贪心地一层一层地剥开你的心...哦不对，一层一层地优化：将结点分类为左孩子和右孩子的得分增益为： \[Gain = \frac{1}{2} \left[\frac{G_L^2}{H_L+\lambda}+\frac{G_R^2}{H_R+\lambda}-\frac{(G_L+G_R)^2}{H_L+H_R+\lambda}\right] - \gamma\] 其中，第一/二项分别表示左/右孩子的分数，第三项表示原始节点的分数，最后一项表示增加叶子的惩罚。可以看到：如果分裂后的得分增益小于\(\gamma\)，就不要继续分了，凑合过吧...

为了在每层获取到最佳的分裂点，通常先将训练数据排个序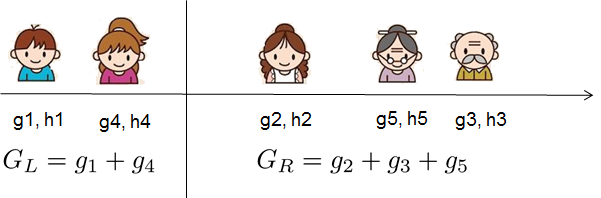：暴力枚举一遍分裂点找最优就可以啦！

\(f_0(x)=0\)
对于第m棵树的训练：
- 首先计算每条训练数据的残差：\(r_{mi}=y_i-f_{m-1}(x_i),i=1,2...,N\)
- 接着通过拟合上面得到的残差数据，训练出回归树\(T_m(x)\)
- 此时第m棵树的输出即为\(f_m(x)=f_{m-1}(x)+T_m(x)\)
进行M次训练后得到最终的模型

可以看到：Boosting Decision Tree每次迭代都将上一轮预测结果的残差作为当前的训练集，对于平方损失容易求得损失函数最小值的点，但是对于稍复杂的损失函数，残差的获得就只能通过负梯度\(\frac{\partial L(y_i,f(x_i))}{f(x_i)}\)去逼近，这就是GBDT的核心思想。 GBDT的训练与Boosting Decision Tree很相似：

初始化弱学习器\(f_0(x)=\underset{c}{arg\ min}\sum_{i=1}^{N}L(y_i,c)\)，如果损失函数是MSE，那么\(f_0(x)=\frac{1}{N}\sum_{i=1}^{N}y_i\)
对于第m棵树的训练：
- 计算负梯度：\(r_{mi}=-\frac{\partial L(y_i,f(x_i))}{\partial f(x_i)},f(x)=f_{m-1}(x)\)
- 得到新的训练集\((x_i,r_{mi})\)，训练产生一棵新的回归树，对应的叶子结点域为\(R_{mj},j=1,...,J\)，\(J\)为叶子结点个数
- 对第j个叶子结点，计算最佳拟合值：\(c_{mj}=\underset{c}{arg\ min}\sum_{x_i\in R_{mj}}L(y_i,f_{m-1}(x_i)+c)\)
- 更新强学习器：\(f_m(x)=f_{m-1}(x)+\sum_{i=1}^{J}c_{mj}I(x\in R_{mj})\)
最终的学习器为：\(\hat f(x)=f_M(x)=f_0(x)+\sum_{m=1}^{M}\sum_{j=1}^{J}c_{mj}I(x\in R_{mj})\)

Implementation

Properties

extrapolate问题
众所周知随机森林回归是不具备推理能力的，那么XGBoost可以吗？
答案是可以，因为梯度提升模型并不直接根据训练集的结果做预测，而是通过一系列树的加和得到，加和结果取决于每棵树的权重，权重则是由损失函数的一二阶梯度优化得来，并不依赖于训练集的上下限。
缺失值问题
GBDT/GBRT自身不支持缺失值的自动填充，例如使用sklearn中的GradientBoostingRegressor在训练数据包含缺失值时将无法训练，人工填充可能会引入偏差，但是XGBoost却可以自动地处理缺失值（但并不是填充）。
根据陈天奇大佬的说法：

Internally, XGBoost will automatically learn what is the best direction to go when a value is missing. Equivalently, this can be viewed as automatically "learn" what is the best imputation value for missing values based on reduction on training loss.

那么究竟是如何自动学习最佳的分裂方向呢？
假设在结点A有50条训练样本，并且该结点只有一个可能的分割点：比如只有一个二元特征x，那么分割点就只有该特征取值为0或1，这样训练数据可以被分为3组：

x取值为B的20条样例
x取值为C的20条样例
x缺失的10条样例，叫做M组

那么M组的样例会被分别赋到B和C，接着计算\(\{(B,M),C\}\)和\(\{B,(C,M)\}\)的得分及损失函数衰减，两者中选择损失函数衰减大的。
如果使用MSE作为损失函数，并且B的标签均值为5，C的标签均值为10，M的标签均值为0。
如果使用\(\{(B,M),C\}\)：\(\frac{|M|}{|B| + |M|}\text{mean}(M) + \frac{|B|}{|M|+|B|}\text{mean}(B) = \frac{10}{30}0 + \frac{20}{30}5 = 3.\overline{3}\)
如果使用\(\{B,(C,M)\}\)：\(\frac{|M|}{|C| + |M|}\text{mean}(M) + \frac{|C|}{|M|+|C|}\text{mean}(C) = \frac{10}{30}0 + \frac{20}{30}10 = 6.\overline{3}\)
最后计算两者的MSE与划分前MSE的差，选择使得MSE下降更快的作为分裂方向（也就是得分gain更大的方向）。

在寻找最优特征分裂点（如年龄＜20还是年龄＜30）时，只访问该特征不含缺失值的训练样例，即如果年龄缺失，就不参与20和30的决策，这样计算复杂度也就降低了，尤其是对于稀疏数据。

预测时的缺失值有２种情况： 1. 训练阶段已经见识过该缺失值了：按照训练时选定的方向往下走就行 2. 训练阶段该特征没有缺失：默认走向右子树。

Ref里还有一个更加全面的例子，训练集有6个小孩，只有一个特征年龄（其中有2个样例年龄缺失），标签是身高，初始预测值为0.5，接下来每棵树都要拟合残差。

Age	Height	Res
7	130	－129.5
9	148	－147.5
6	115	－114.5
15	164	－163.5
？	125	－124.5
？	140	－139.5

接着要根据年龄特征寻找最优的分裂点，将年龄排序并选择中点（注意：这里就不考虑缺失值样例了），因此候选分裂点有6.5，8，12，对于每个候选点，分别计算将缺失样例划到左子树和右子树的Quality/Similarity Score：

\[ Quality\ Score=\frac{(\sum residuals)^2}{\#residuals + \lambda} \]

比如，对于分裂点6.5：
如果划到左子树： \[ Gain＝划分后的Quality\ Score－划分前的Quality\ Score \\ ＝\frac{(-114.5-124.5-139.5)^2}{3} + \frac{(-129.5-147.5-163.5)^2}{3} - \frac{(-129.5-147.5-114.5-163.5-124.5-139.5)^2}{6}=640.7 \]
如果划到右子树：\(Gain＝划分后的Quality\ Score－划分前的Quality\ Score＝580.8\)

接着对于8：1083；630.8
对于12：874.8；216
从中选择gain最大的（也就是使得损失函数最小的），分裂点选8，缺失值划到左子树。