为了在统一框架里分析周期信号与非周期信号,可以给周期信号也建立傅里叶变换。
有两种方法求周期信号的傅里叶变换:
利用傅里叶级数进行构造
对于周期信号\(x(t)\),其傅里叶级数展开式为: \[x(t) = \sum_{k = -\infty}^{+\infty}a_ke^{jkw_0t}\] 系数\(a_k\)表示为:
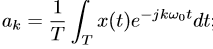
由于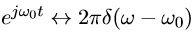
说明周期性复指数信号的频谱是一个冲激,那么我们推广这个关系,可得: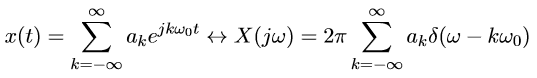
表明:周期信号的傅里叶变换由一系列等间隔的冲激函数线性组合而成,每个冲激分别位于信号各次谐波的频率处,其强度是傅里叶级数系数的\(2\pi\)倍。周期延拓
这种方法先将\(x(t)\)在一个周期内截断,得信号\(x_T(t)\),求出\(x_T(t)\)的傅里叶变换\(X_T(w)\),再对\(X_T(w)\)周期延拓得\(X(w)\)。
具体来说:
根据\(\delta\)函数性质,有: \[x(t) = x_T(t)*\sum_{k = -\infty}^{+\infty}\delta(t - kT)\] 设周期冲激串\(\sum_{k = -\infty}^{+\infty}\delta(t - kT)\)的傅里叶变换为\(F(w)\),
由时域卷积定理: \[X(w) = X_T(w)F(w)\] 又时域周期为T的周期冲激串的傅里叶变换在频域是一个周期为\(\frac{2\pi}{T}\)的周期冲激串,即: \[F(w) = \frac{2\pi}{T}\sum_{k = -\infty}^{+\infty}\delta(w - \frac{2\pi k}{T})\] 故可得: \[X(w) = \frac{2\pi}{T}X_T(w)\sum_{k = -\infty}^{+\infty}\delta(w - \frac{2\pi k}{T})\] 也就是: \[X(w) = w_0\sum_{k = -\infty}^{+\infty}X_T(kw_0)\delta(w - kw_0)\] 我们对比两种方法得到的结果,可知:
周期信号傅里叶级数的系数\(a_k = \frac{1}{T}X_T(kw_0)\)

