EI Madrigal's Space
0%

CS231n Assignment

Posted on Edited on In
Convolutional Neural Networks for Visual Recognition

先吹一波Google Colab，所有操作都可在云上进行，还能白嫖🐕家的GPU；再吹一下Stanford的骨架代码，真的是干净整洁优美，堪称典范。
My Code

kNN

最幼稚的机器学习算法。

  1. 计算测试集和训练集的距离
    训练集X_train的shape为\((N, D)\)，y_train的shape为\((N,)\)，y[i]取值范围\([0,C-1]\)
    测试集X_test的shape为\((M, D)\)，最终的distance matrix的shape为\((M,N)\)
    声明：不能使用类似于np.linalg.norm()这种东西作弊。
    首先来看看2重循环：第一重遍历测试集，第二重遍历训练集，当然如果你愿意，还可以用第三重遍历dimension去累加距离；
    再来看看只遍历测试集的单层循环：对于每个测试样例X[i]，减去X_train，通过广播机制得到一个\((N, D)\)的差矩阵，做element-wise的平方，按列相加得到\((N,)\)，表示测试样例X[i]与每个训练样例的距离，作为距离矩阵的第\(i\)行；
    最后来看看full-vectorized的版本，数学推导见NumPy之计算两个矩阵的成对平方欧氏距离，吃饱没事干的同学可以自己推推，我数学太差就溜了。
  2. 根据距离矩阵预测测试集的标签
    对于每个测试样例X[i]，选k个距离最小的训练样例，将其label（从y_train获得）存入cloest_y中，投票决定最终的预测标签。
    先用idx=np.argsort(dists[i])[:k]取出前k个训练样例的index，再用y_train[idx]得到对应的k个label，最后用np.argmax(np.bincount(cloest_y))得到最终的预测label。

kNN效果当然比较拉垮了，在CIFAR-10的子集上分类正确率大概在27%左右。比较令我震惊的是三个计算距离函数耗费的时间，2重循环57s，单层循环41s，fully-vectorized只有0.57s，竟然降低了100倍，写出高效的代码对于程序性能有着至关重要的影响，反思下自己写出的junk code，不由得留下了伤心的泪水...

最后就是用cross-validation确定超参k的取值，就略过了哈。

Linear Multiclass SVM

首先要为多分类SVM写一个损失函数，老规矩还是先写一个naive版本svm_loss_naive(W, X, y, reg)：
权重矩阵W：\((D, C)\)
minibatch输入X：\((N, D)\)
标签y：\((N,)\)，y[i]=c表示X[i]的标签是c，\(0 \leq c<c\)
返回浮点数loss和解析梯度dw
Multiclass Support Vector Machine loss是这么定义的：
\[L = \frac{1}{N} \sum_i \sum_{j\neq y_i} \left[ \max(0, f(x_i; W)_j - f(x_i; W)_{y_i} + \Delta) \right] + \lambda \sum_k\sum_l W_{k,l}^2\] 看着有点复杂哦！主要有data loss和正则项两部分，对于第\(i\)个训练样本，data loss为：
\[L_i = \sum_{j\neq y_i} \max(0, s_j - s_{y_i} + \Delta),s_j = f(x_i, W)_j\] 什么意思呢？\(s\)是第\(i\)个训练样本的得分向量\((C,)\)，\(s_{y_i}\)表示正确标签的得分，\(s_j\)表示其他类的得分。不妨看看什么时候损失为0呢？稍作变形即有：当\(s_{y_i}-s_j>\Delta\)时，第\(j\)类损失为0，说人话就是只有当正确类的得分减去其他类的得分大于某个间隔\(\Delta\)时才不会累积损失，否则就累加损失（必然为正数），这就是大名鼎鼎的Hinge Loss。

如果\(f\)用的是linear score function，进一步有： \[L_i = \sum_{j\neq y_i} \max(0, w_j^T x_i - w_{y_i}^T x_i + \Delta)\] 其中，\(w_j\)表示W的第\(j\)列。
至此，naive版本的loss实现就不必废话了。接着来求dW，老规矩，还是先研究单个样本。

如果你的数学还行，下面的梯度推导可以略过： \[L_i = max(0,w_1^T x_i - w_{y_i}^T x_i + \Delta)+max(0,w_2^T x_i - w_{y_i}^T x_i + \Delta)+...+max(0,w_C^T x_i - w_{y_i}^T x_i + \Delta)\] 共有\(C-1\)项，因为\(j=y_i\)那项不算。另，只有在\(w_j^T x_i - w_{y_i}^T x_i + \Delta>0\)时第\(j\)项的梯度不为0。

  1. 对\(w_{y_i}\)的梯度
    每项都有，并且都是0或\(-x_i\)，因此只要看几项大于0，梯度就是几倍的\(-x_i\)，正式点就是： \[\nabla_{w_{y_i}} L_i = - \left( \sum_{j\neq y_i} \mathbb{1}(w_j^Tx_i - w_{y_i}^Tx_i + \Delta > 0) \right) x_i\]
  2. 对\(w_j\)的梯度
    只有第\(j\)项有，0或\(x_i\)，正式点就是： \[\nabla_{w_j} L_i = \mathbb{1}(w_j^Tx_i - w_{y_i}^Tx_i + \Delta > 0) x_i\]

naive版本的dW[:,j]和dW[:,y[i]]就2重循环按部就班更新即可，别忘了除以\(N\)和正则项梯度。

接着来实现svm_loss_vectorized(W, X, y, reg)：

  1. loss
    首先求得整个训练集的得分矩阵scores，shape为\((N,C)\)，每一行表示一个样例的得分。正确类得分向量correct_class_score可用scores[np.arange(num_train), y]得到，shape为\((N,)\)，注意这里不能用scores[:, y]，简单试验下：
1
2
3
4
X = np.array([[1,2,3],[3,4,5]])
y = np.array([2, 1])
print(X[np.arange(2), y])  # [3,4]
print(X[:, y])  # [[3,2],[5,4]]

下来到了最关键的margins矩阵，该矩阵和scores矩阵shape相同\((N,C)\)，第\(i\)行表示第\(i\)个训练样本的margin即\(max(0,s_j - s_{y_i} + \Delta)\)，在每一行第\(y_i\)个位置上应当设置为0，其余位置按照公式即可：

1
2
margins = np.maximum(0, scores - correct_class_score[:, np.newaxis] + 1)
margins[np.arange(num_train), y] = 0

需要注意：correct_class_score是一个\((N,)\)的向量，如果直接scores-correct_class_score就会报错，广播机制从最后一个维度开始比对，只有相等或者其中某个为1才行，因此用np.newaxis将correct_class_score的shape变为\((N,1)\)；还有就是np.max()和np.maximum()的区别，np.max()和np.amax(a, axis=None, ...)等价，返回数组的最大值，np.maximum(x1, x2, out=None, ...)返回element-wise的较大值。

  1. 梯度
    这里也稍微有点tricky，根据naive版本对梯度的讨论：对\(w_j\)的梯度需要知道margin的正负，对\(w_{y_i}\)的梯度需要知道有几项大于0。怎么借助margins矩阵统计每一行大于0的项数呢？无聊的程序员先将矩阵中大于0的项都设为1，然后按列相加即可：
1
2
3
margins[margins > 0] = 1.0
num_to_loss = np.sum(margins, axis=1)  # (N,)
margins[np.arange(num_train, y)] = -num_to_loss

对单个样本\(i\)来说，其对dW的贡献要么是在第\(j\)列（即第\(j\)个类）加上\(x_i\)，要么在第\(y_i\)列加上\(-kx_i\)，\(k\)为margins[i]中大于0的元素个数，即num_to_loss[i]，整个训练集对dW的更新即是在累加单个样本对dW每一列（每个类）的影响。对第\(j\)列，其更新即为每个训练样本对该类贡献的线性组合，组合系数取决于该样本的标签以及是否满足指示函数，即为margins的第\(j\)列，取值范围\(\{0,1,-k\}\)，0表示该样本对第\(j\)个类的梯度没有贡献（该样本标签不是\(j\)且不满足指示函数），1表示贡献了\(x_i\)（该样本标签不是\(j\)且满足指示函数），\(-k\)表示贡献了\(-kx_i\)（该样本的标签就是\(j\)），因此：

1
dW = np.dot(X.T, margins) / num_train + 2 * reg * W

可以从矩阵维度相容的角度验证。

Softmax

先用循环实现一个softmax_loss_naive(W, X, y, reg)，输入的shape和SVM相同。
softmax分类器不再将\(f(x_i;W)\)看做每个类的得分，而是希望输出normalized class probabilities，最终选一个概率最大的类作为预测，softmax函数就能将\(f(x_i;W)\)映射到\([0,1]\)且满足概率的性质： \[P(y_i \mid x_i; W) = \frac{e^{f_{y_i}}}{\sum_j e^{f_j} }\] 从预测函数可以看到：softmax是把\(f(x_i;W)\)看作unnormalized log probabilities，因此对\(f(x_i;W)\)先指数再归一化得到每个类的概率。

再来看softmax的损失函数： \[L_i = -\log\left(\frac{e^{f_{y_i}}}{ \sum_j e^{f_j} }\right) \hspace{0.1in} \text{or equivalently} \hspace{0.1in} L_i = -f_{y_i} + \log\sum_j e^{f_j}\] 从直觉上说：属于正确类\(y_i\)的概率（括号里的分式）越高，损失应该越小，这就是大名鼎鼎的cross-entropy loss，衡量了真实分布\(p\)和预测分布\(q\)之间的差距： \[H(p,q) = - \sum_x p(x) \log q(x)= H(p) + D_{KL}(p||q)\] 具体到softmax： \[q=\frac{e^{f_{y_i}}}{ \sum_j e^{f_j} },p = [0, \ldots 1, \ldots, 0]\] 其中，\(p\)在第\(y_i\)个位置上为1。
由于\(H(p)=0\)，因此其实是在最小化\(p\)和\(q\)的KL散度，即希望预测结果\(q\)尽量向\(p\)靠近。

从概率的角度出发看损失函数，我们是在最小化正确类\(y_i\)的负对数似然，本质上就是在做一个极大似然估计。

看完理论，还要考虑一些现实问题。比如数值稳定性，由于指数的原因可能会导致overflow或者underflow，因此做一个简单的等价变换： \[\frac{e^{f_{y_i}}}{\sum_j e^{f_j}} = \frac{Ce^{f_{y_i}}}{C\sum_j e^{f_j}} = \frac{e^{f_{y_i} + \log C}}{\sum_j e^{f_j + \log C}}\] 一般选\(\log C = -\max_j f_j\)，这个变换不会改变预测函数或者损失函数，只是将得分做了平移。

至此，naive版本的loss就基本有了，接着看看梯度咋求。先稍稍展开康康： \[L_i=-f_{y_i} + \log\sum_j e^{f_j}=-w_{y_i}^Tx_i+log\sum_je^{w_j^Tx_i}\] 其中，\(w_j\)表示W的第\(j\)列。
然后使用我们的小学数学知识去求偏导： \[\nabla_{w_{y_i}} L_i =(\frac{e^{f_{y_i}}}{ \sum_j e^{f_j}}-1)x_i \\ \nabla_{w_j} L_i = \frac{e^{f_{j}}}{ \sum_j e^{f_j}}x_i\] 记p = np.exp(scores) / np.sum(np.exp(scores))，shape为\((C,)\)，表示样本\(i\)属于每个类的概率。
所以dW的第y[i]列更新即为(p[y[i]] - 1) * X[i]，其他列更新为p[j] * X[i]。

接着看下vectorized版本，scores的shape变为了\((N,C)\)，首先处理数值稳定性问题，每一行都减去该行的最大值（注意keepdim=True）；接着求出概率矩阵p，shape与scores相同，那么loss为：
loss = np.sum(-np.log(p[np.arange(X.shape[0]), y])) / X.shape[0]
与SVM类似，dW的每一列（每个类）是由每个训练样本影响的线性组合决定的，组合系数取决于该训练样例的标签，比如对于dW的第\(j\)个类来说，如果某个样例的标签恰好是\(j\)，那么其对梯度的贡献就是p[j]-1，否则系数就是p[j]。因此只要将概率矩阵p中所有正确标签的值减1即得到系数矩阵，进而得到dW：

1
2
p[np.arange(X.shape[0]), y] = p[np.arange(X.shape[0]), y] - 1
dW = np.dot(X.T, p)

同样可以用维度相容去check。

Neural Network

这是一个两层的全连接神经网络，架构如下：
输入\((N,D)\)->全连接层1->ReLU->全连接层2（输出每个类的得分）->softmax
参数们的shape为：\(X(N,D),W1(D,H),b1(H,),W2(H,C),b2(C,)\)

第一步Forward Pass，根据输入X和权值W计算\(scores(N,C)\)，然后计算softmax loss；
第二步Backward Pass，需要计算loss对于参数们的梯度，根据网络结构： \[h=XW1+b1\\ o=ReLU(h)\\ s=oW2+b2\\ L=\sum_i(-s_{y_i}+log\sum_j e^{s_j})\] 根据链式法则+维度相容： \[\nabla_{w_2} L =o^T \nabla_{s} L\\ \nabla_{b_2} L =(\nabla_{s} L)^T(\nabla_{b_2} s)=(C,N)(N,1)=(C,N)(all\ 1\ col)\\ \nabla_{w_1} L =X^T \nabla_{s} L\nabla_{h} s\\ \nabla_{b_1} L =\nabla_{h} s (\nabla_{s} L)^T\nabla_{b_1} h=(H,C)(C,N)(N,1)=(H,C)(C,N)(all\ 1\ col)\] 可以看出：关键在于求出\(\nabla_{s} L\)，在对softmax的讨论中可知，对于第\(y_i\)列导数为p[y[i]]-1，对其他列为p[j]，因此该偏导为：

1
2
d2 = p
d2[np.arange(X.shape[0]), y] -= 1

另外对于\(W_1,b_1\)，还需要\(\nabla_{h} s\)：这玩意在\(h>0\)就是\(W_2^T\)，否则就是0。因此\(\nabla_{s} L\nabla_{h} s\)可以写为：

1
d1 = d2.dot(W2.T) * (h > 0)

Image Features

之前的样例都是直接用raw pixel，加上都是线性模型，效果拉跨太正常了。这里用的人工feature包括HOG(Histogram of Oriented Gradients)和color histogram，HOG捕捉texture（纹理变化？）信息，color histogram捕捉颜色信息，两者互相辅助。

Fully-connected Neural Network

我好菜啊！！很早就写完代码了，gradient check也过了，但是需要过拟合50张图片的时候一直不太对，调了几下学习率，我看train acc只有0.14左右，loss曲线波动也很大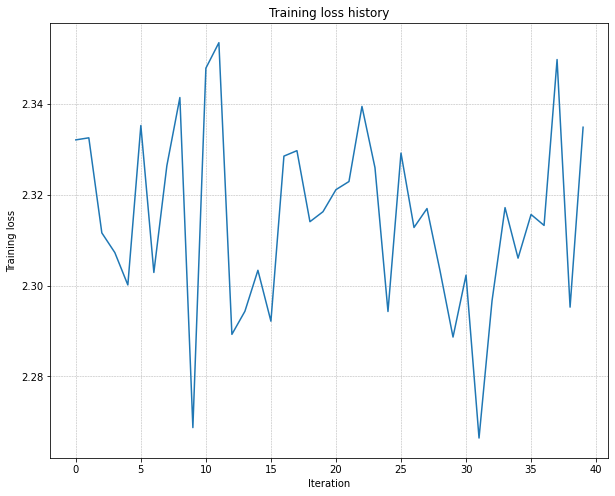： image 因为最后要100%的train acc嘛，我看差的挺远的，就开始怀疑是网络哪里写错了，就没管超参数，检查代码检查了好几天tmd，深度学习debug还真是无从下手...后来跑去看了下别人的东西，发现原因竟然是不会调参(T^T)。

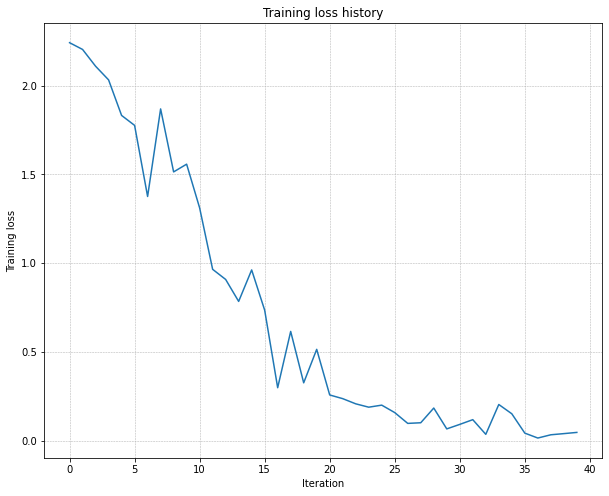
仔细看下，这里还是很明显的，20个epoch训练损失才下降了一点点，说明学习率太小了。 image