EI Madrigal's Space
0%

Binary Indexed Tree

Posted on Edited on In
树状数组

引言

LeetCode 307这道题给一个可修改的数组，需要进行频繁的区域和检索。
一个naive的做法是，每次查询都从\(i\)累加到\(j\)： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class NumArray {
public:
    NumArray(vector<int>& nums) {
        nums_ = nums;
    }
    
    void update(int i, int val) {
        nums_[i] = val;
    }
    
    int sumRange(int i, int j) {
        int ans = 0;
        for (int k = i; k <= j; ++k)
            ans += nums_[k];
        return ans;
    }
private:
    vector<int> nums_;
};
这种方法每次更新的复杂度为\(O(1)\)，单次查询的复杂度为\(O(n)\)。

树状数组

树状数组可以在\(O(lgn)\)时间复杂度内完成上述两个操作：

  1. 单点更新
  2. 计算前缀和并进行区间查询

BIT并不需要定义树的结点和指针，而是维护了一个特殊的前缀和数组prefix_sum_，下面的例子均是1-indexed，调用BIT时需要传入原始索引+1。填充prefix_sum_的过程是这样的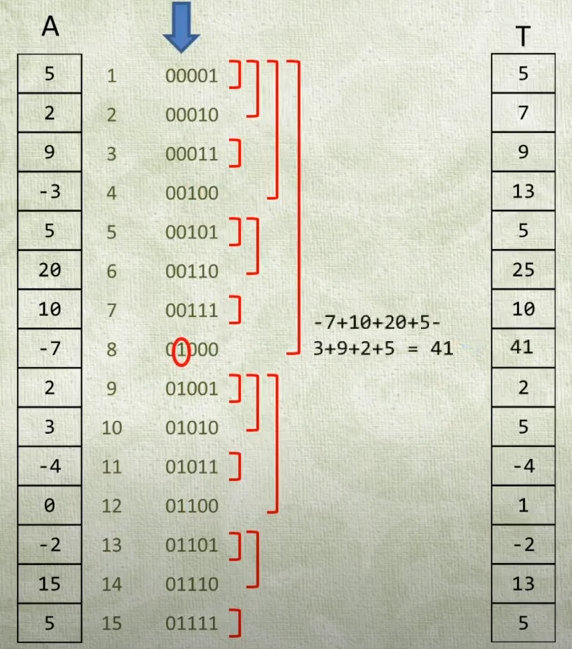： 在这里插入图片描述 1. 按照索引的二进制表示，先看最低位，将所有最低位为1的数值直接存入T 2. 再看次低位为1的（即10结尾的），将该数和前一个数（共2个数）的和存入T 3. 再看以100结尾的，将该数及之前的3个数（共4个数）的和存入T 4. 再看以1000结尾的，将8个数的和存入T，以此类推...

填充好prefix_sum_后，就可以查询原始数组的前缀和并且更新原始数组。

查询

假设要求前缀和A[1]+...+A[7]即query(7)，只需要query(7)+query(6)+query(4)即可，从二进制来看就是query(00111)+query(00110)+query(00100)，即每次将最后一位1翻转然后累加直到i变为0。

更新

假设要更新A[4]即update(4, 10)，需要更新T[4]和T[8]，即00100和01000，即每次将最后一位1左移直到i超出数组长度，移位过程中更新相应的T[i]。

填充prefix_sum_可以直接调用update。

那么我们的tree： 在这里插入图片描述 0是dummy node，将结点的二进制表示的最后一个1翻转，就能得到其父结点。

下来填充这棵树： \(1=0+2^0\)，存储从下标0开始的前1个数的和：3（0，0）； \(2=0+2^1\)，存储从下标0开始的前2个数的和：5（0，1）； \(3=2^1+2^0\)，存储从下标2开始的前1个数的和：-1（2，2）； \(4=0+2^2\)，存储从下标0开始的前4个数的和：10（0，3）； \(5=2^2+2^0\)，存储从下标4开始的前1个数的和：5（4，4）； \(6=2^2+2^1\)，存储从下标4开始的前2个数的和：9（4，5）； \(7=2^2+2^1+2^0\)，存储从下标6开始的前1个数的和：-3（6，6）； \(8=0+2^3\)，存储从下标0开始的前8个数的和：19（0，7）； \(9=2^3+2^0\)，存储从下标8开始的前1个数的和：7（8，8）； \(10=2^3+2^1\)，存储从下标8开始的前2个数的和：9（8，9）； \(11=2^3+2^1+2^0\)，存储从下标10开始的前1个数的和：3（10，10）； 填充后的tree： 在这里插入图片描述 接下来就可以根据这棵树来计算prefixSums_： 假如要计算\(0-5\)的和，从下标6出发，一直加到dummy node，得到prefixSums_[6]=9+10=19； 要计算\(0-9\)的和，从下标10出发，一直加到dummy node，得到prefixSums_[10]=9+19=28。 以计算\(0-9\)的和为例，结点10存储的是（8，9）的部分和，结点8存储的是（0，7）的部分和，所以加起来就是\(0-9\)的和。

快速实现

上面求结点的父结点、将下标拆解为二进制去填充树的方式很慢，来看一种稍快的方式。 查询时，我们需要计算从某结点到dummy node的和，这就涉及计算该结点的parent： 假如要求结点7的parent，7的二进制原码为111，-7的补码为001，将原码和补码按位与得001，用原码减去001，得110=6，即7的父结点是6。 更新时，我们需要更新所有包含该结点的部分和结点： 假如更新了结点1，1的二进制原码为001，-1的补码为111，将原码和补码按位与得001，用原码加上001，得010=2，即还要更新结点2，更新了结点2，还要更新结点4...... 最后来看下非常简洁的实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
// 一维
class BIT {
private:
    vector<int> prefix_sum_;
    static inline int lowbit(int x) {
        return x & (-x);
    }
public:
    BIT(int n) : prefix_sum_(n + 1, 0) {}

    void update(int i, int delta) {
        while(i < prefix_sum_.size()) {
            prefix_sum_[i] += delta;
            i += lowbit(i);  // add last set bit
        }
    }

    // compute nums[0] + nums[1] + ... + nums[i - 1]
    int query(int i) {
        int sum = 0;
        while(i > 0) {
            sum += prefix_sum_[i];
            i -= lowbit(i);  // flip the last set bit
        }
        return sum;
    }
};

// 二维
class BIT {
public:
    BIT(int m, int n) : prefix_sum_(m + 1, vector<int>(n + 1, 0)) {}

    void update(int i, int j, int delta) {
        for (int x = i; x < prefix_sum_.size(); x += lowbit(x))
            for (int y = j; y < prefix_sum_[0].size(); y += lowbit(y))
                prefix_sum_[x][y] += delta;
    }

    int query(int i, int j) {
        int ans = 0;
        for (int x = i; x > 0; x -= lowbit(x))
            for (int y = j; y > 0; y -= lowbit(y))
                ans += prefix_sum_[x][y];
        return ans;
    }

private:
    vector<vector<int>> prefix_sum_;  // 一维维护的是一个前缀和数组，二维维护一个前缀和矩阵
    static inline int lowbit(int x) {
        return x & (-x);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class NumMatrix {
public:
    NumMatrix(vector<vector<int>>& matrix) : matrix_(matrix), tree_(matrix.size(), matrix[0].size()) {
        for (int i = 0; i < matrix.size(); ++i) {
            for (int j = 0; j < matrix[0].size(); ++j) {
                tree_.update(i + 1, j + 1, matrix[i][j]);
            }
        }
    }

    void update(int row, int col, int val) {
        tree_.update(row + 1, col + 1, val - matrix_[row][col]);
        matrix_[row][col] = val;
    }

    int sumRegion(int row1, int col1, int row2, int col2) {
        return tree_.query(row2 + 1, col2 + 1) + tree_.query(row1, col1) - tree_.query(row1, col2 + 1) - tree_.query(row2 + 1, col1);
    }
private:
    vector<vector<int>> matrix_;
    BIT tree_;
};

// Your NumMatrix object will be instantiated and called as such:
// NumMatrix numMatrix(matrix);
// numMatrix.sumRegion(0, 1, 2, 3);
// numMatrix.update(1, 1, 10);
// numMatrix.sumRegion(1, 2, 3, 4);

Reference

Fenwick Tree or Binary Indexed Tree
花花酱 Fenwick Tree / Binary Indexed Tree SP3
Fenwick Tree