贝叶斯学习

简介

贝叶斯概率理论是由Thomas Bayes在1764年提出，采用一种概率的方式进行推理。贝叶斯学习有2个假设： - 观察到的样本实例并非确定性事件，而是随机的，服从某种概率分布； - 通过对观测数据样本和相关的概率特性进行推理学习能够得到最优的决策或分类。

贝叶斯学习为衡量多个假设的置信度提供了定量的方法，其依赖于贝叶斯决策理论（Bayesian Decision Theory）。贝叶斯决策理论是一种统计学上的方法，用来定量化地描述使用概率做出的不同决策以及这些决策付出的代价之间的权衡。首先假设一些概率值是已知的，然后根据这些已知概率推理一些未知情况下的概率值，最终利用这些推理的概率值进行决策。

以分类问题为例，假设有2种鱼分别是鲑鱼和鲈鱼，将w定义为观测到的鱼的类型，令\(w=w_1\)代表鲈鱼，\(w=w_2\)代表鲑鱼，定义\(P(w_1)\)表示下一条鱼是鲈鱼的先验概率，\(P(w_2)\)表示下一条鱼是鲑鱼的先验概率。先验概率反映了人们根据经验和背景知识对事物的判断，即在看到下一条鱼之前对于\(P(w_1)\)和\(P(w_2)\)的判断。如果没有经验上的偏好，就可以设置为均匀先验\(P(w_1)=P(w_2)\)；如果有诸如海域因素、时间等背景，便可以为\(P(w_1)\)和\(P(w_2)\)设置不同的先验概率。另外假设只有这2种鱼，即\(P(w_1)+P(w_2)=1\)。在仅有先验概率的情况下，选择先验概率大的作为最终决策，这种情况下决策错误的概率为\(min\{P(w_1),P(w_2)\}\)。

贝叶斯决策理论是很多重要的学习算法的基础，例如朴素贝叶斯分类器、贝叶斯信念网络以及EM算法等。另外，贝叶斯决策理论为许多非贝叶斯的学习算法提供了很好的数学和框架性理论基础，对某些学习任务而言，贝叶斯学习是最实用的方法之一。

贝叶斯学习有以下特点： - 每个观测到的训练样本都可以很小程度上增大或减小某个假设正确的概率； - 先验知识可以和观测数据结合起来决定某个假设的最终概率，可以计算显式的假设概率； - 新实例的预测可以结合多个假设输出概率的加权值； - 通常需要一些背景知识或先前经验来确定先验概率，选出贝叶斯最优分类器计算代价比较大。

贝叶斯定理

贝叶斯定理是贝叶斯学习的基石，给定训练数据集D，在假设空间H中寻找最优的假设h，最优假设可以定义为给定数据集D以及H中不同假设的先验概率条件下的最可能的假设。利用贝叶斯定理，在已知假设的先验概率、观测数据以及给定假设下观测到特定数据的概率就可以计算出最有可能的假设。

给定数据集D以及假设空间H，定义如下记号： - 先验概率P(h)：没有训练数据前假设h的初始概率，反映了根据人们的相关认知背景，假设h成为正确假设的概率，如果没有先验知识，可以将每一个候选假设的先验概率设置为相同的。 - 先验概率P(D)：训练数据D的先验概率，即不知道哪个假设成立的前提下观测到D的概率。 - 观测数据的条件概率P(D|h)：在假设h成立的条件下观测到数据集D的概率。 - 后验概率P(h|D)：给定观测到的训练数据集D时假设h成立的概率，反映了观测到的训练数据是D时h成立的置信度。

利用贝叶斯定理可以计算给定训练数据集D下任一假设的后验概率： \[P(h|D)=\frac{P(D|h)P(h)}{P(D)}\]

贝叶斯推理得到的结果很大程度上依赖于先验概率，并且不是完全接受或拒绝假设h，而是给出假设为真的可能性。因此可以计算每个假设的概率，输出其中概率最大的，称为最大后验概率准则（Maximum A Posteriori）。

\[ h_{MAP}=\underset{h\in H}{\operatorname{\argmax}}\ P(h|D) \\ =\underset{h\in H}{\operatorname{\argmax}}\ \frac{P(D|h)P(h)}{P(D)} \\ =\underset{h\in H}{\operatorname{\argmax}}\ P(D|h)P(h) \]

如果假设空间中每个假设的先验概率都是相同的，即\(P(h_i)=P(h_j),\forall h_i\in H \wedge \forall h_j\in H\)，那么只需要考虑给定假设h下数据D的似然P(D|h)，这样最大后验概率准则就变为了最大似然估计（Maximum Likelihood）： \[ h_{ML}=\underset{h\in H}{\operatorname{\argmax}}\ P(D|h) \]

最小描述长度原则

根据奥卡姆剃刀原则，其它条件相同时选择最简单的假设，最简单的假设可以定义为描述长度最小的假设，即给定假设空间H和数据集D，应该寻找一个假设或者假设组合使得D被最大程度地压缩。定义\(L_{C}(x)\)表示在编码机制C下编码x需要的最少的比特数为编码机制C下的x的描述长度。 \[ h_{MDL}=\underset{h\in H}{\operatorname{\argmin}}\ L_{C_1}(h)+L_{C_2}(D|h) \]

\(L_{C_1}(h)\)是假设的描述长度即比特数，反映了模型的复杂程度；\(L_{C_2}(D|h)\)是当采用假设h编码后数据的描述长度，反映了错误的数目。通常会发现：一个非常复杂的假设（\(L_{C_1}(h)\)大）会有一个比较好的拟合（\(L_{C_2}(D|h)\)小），反之一个非常简单的假设（\(L_{C_1}(h)\)小）会有比较差的拟合（\(L_{C_2}(D|h)\)大）。因此希望寻找一个假设：既不会过于复杂同时还可以对数据有比较好的拟合。

如果对MAP的公式进行变形： \[ h_{MAP}=\underset{h\in H}{\operatorname{\argmax}}\ P(D|h)P(h) \\ =\underset{h\in H}{\operatorname{\argmax}}\ log_2P(D|h)+log_2P(h) \\ =\underset{h\in H}{\operatorname{\argmin}}\ -log_2P(h)-log_2P(D|h) \\ \]

可以看到：第一项\(-log_2P(h)\)对应了最优编码机制\(C_1\)下h的描述长度\(L_{C_1}(h)\)，第二项\(-log_2P(D|h)\)对应了最优编码机制\(C_2\)下数据的描述长度\(L_{C_2}(D|h)\)。两者的优化目标是一致的。

贝叶斯最优分类器

通过MAP准则可以求出在给定训练数据下的最有可能的假设，那么如何求出给定训练集下一个新实例的最优预测呢？可以对新实例使用MAP准则，求得最大的假设然后进行分类。

但是最优的结果应该是结合所有假设的预测结果对新实例进行分类，结合的方法是通过后验概率加权： \[ \underset{v_j\in V}{\operatorname{\argmax}}\ \sum_{h_i\in H}P(v_j|h_i)P(h_i|D) \]

V表示所有可能的预测结果，\(v_j\)是其中一种预测分类。\(P(v_j|h_i)\)表示假设\(h_i\)将新实例预测为\(v_j\)的概率大小，\(P(h_i|D)\)表示假设\(h_i\)的后验概率。

例如假设空间\(H=\{h_1,h_2,h_3\}\)，可能的预测结果\(V=\{+,-\}\)，对于一个新实例假设有： \[ P(h_1|D)=0.4, P(-|h_1)=0, P(+|h_1)=1 \\ P(h_2|D)=0.3, P(-|h_2)=1, P(+|h_2)=0 \\ P(h_3|D)=0.3, P(-|h_3)=1, P(+|h_3)=0 \\ \]

那么有： \[ \sum_{h_i\in H}P(+|h_i)P(h_i|D)=0.4 \\ \sum_{h_i\in H}P(-|h_i)P(h_i|D)=0.6 \\ \] 因此最终选择将新实例分类为-。

可以看到：贝叶斯最优分类器最大化了新实例被正确分类的概率，在使用相同假设空间和先验知识的条件下，没有其他方法比贝叶斯最优分类器的平均效果好，最终的预测结果可能对应一个不包含于\(H\)的假设。

虽然效果很好，但是贝叶斯最优分类器计算代价非常大： - 需要遍历假设空间中的所有假设； - 当假设空间非常大时这种方式是不可行的。

因此可以通过吉布斯算法（Gibbs）解决。吉布斯算法根据假设的后验概率分布随机选取一个假设对新实例进行分类。可以证明：在特定条件下，该方法的期望误差最多是贝叶斯最优分类器的两倍。还可以通过采样多个假设并求其预测结果的平均值来提高吉布斯算法的性能，例如可以使用马尔科夫蒙特卡洛采样（MCMC）。

Bagging分类器

虽然可以使用吉布斯算法来降低计算代价，但是从后验概率分布P(h|D)采样是比较困难的： - P(h|D)的计算本身就比较困难 - 对于不是基于概率的分类器例如SVM等P(h|D)是无法计算的 - 当假设空间很大时P(h|D)计算结果会很小

为了解决上述问题，引入Bagging的思想，通过对训练样本的采样实现对后验分布P(h|D)的采样。假设给定的数据集D包含m个样本，自助采样法（Bootstrap sampling）步骤如下： - 从D中有放回地采样m个样本构成数据集\(D^i\) - D中大约有37%的样本不会被采样到

Bagging算法步骤如下： - 创建k个自助采样的数据集\(D^1,D^2,...,D^k\) - 在每个数据集\(D^i\)独立训练分类器\(h_i\) - 通过相等权重的投票法来对新实例进行分类：

\[ c^*(x)=\underset{c}{\operatorname{\argmax}}\ \sum_{i=1}^{k}P(c|h_i,x) \] 由于自助采样法几乎和直接从后验概率分布P(h|D)采样相同，因此Bagging产生的分类器也近似于贝叶斯最优分类器。通常Bagging产生的分类器效果要优于单独的分类器，因为其有效地降低了模型的方差。

朴素贝叶斯分类器

假设训练集D中的每条实例x均可以被n个属性的组合\(<a_1,a_2,...,a_n>\)描述，并且\(v(x)\in V\)是一个有限的集合。那么贝叶斯方法对于新实例的分类是选择一个最有可能的目标值： \[ v_{MAP}=\underset{v_j\in V}{\operatorname{\argmax}}\ P(v_j|a_1,a_2,...,a_n) \]

通过贝叶斯定理进行变形： \[ v_{MAP}=\underset{v_j\in V}{\operatorname{\argmax}}\ \frac{P(a_1,a_2,...,a_n|v_j)P(v_j)}{P(a_1,a_2,...,a_n)} \]

那么要如何计算\(P(v_j)\)和\(P(a_1,a_2,...,a_n|v_j)\)呢？ - \(P(v_j)\)可以通过每个目标值\(v_j\)在训练数据中出现的频率来估算 - 在训练数据集很小的情况下，\(P(a_1,a_2,...,a_n|v_j)\)的估算是不可能的，不同的\(P(a_1,a_2,...,a_n|v_j)\)的数目等于所有可能的目标值的数量与所有可能的样本数目的乘积。

为了解决上述问题，提出了朴素贝叶斯假设，即在给定目标值下样本属性之间是条件独立的： \[ P(a_1,a_2,...,a_n|v_j)=\prod_{i}P(a_i|v_j) \]

因此朴素贝叶斯分类器即为： \[ v_{NB}=\underset{v_j\in V}{\operatorname{\argmax}}\ P(v_j)\prod_{i}P(a_i|v_j) \]

其中，\(v_{NB}\)是朴素贝叶斯分类器的预测输出，\(P(a_i|v_j)\)是训练数据中目标值\(v_j\)时属性\(a_i\)的频率。不同的\(P(a_i|v_j)\)的数目等于不同的目标值数量与属性数量的乘积，该数值远小于不同的\(P(a_1,a_2,...,a_n|v_j)\)的数目。

下面举一个朴素贝叶斯分类器的例子，假设训练数据如下：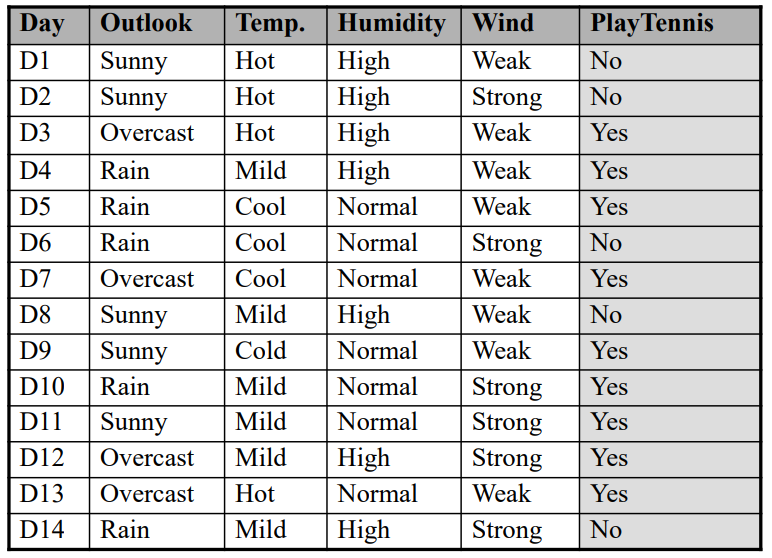

需要对于一个新实例{Outlook=sunny, Temperature=cool, Humidity=high, Wind=strong}进行分类，所有可能的目标值是{yes, no}。因此分类器为： \[ v_{NB}=\underset{v_j\in \{yes,no\}}{\operatorname{\argmax}}\ P(v_j)\prod_{i}P(a_i|v_j) \]

从训练数据可知，\(P(v_j)\)即不同目标值的概率为： \[ P(yes)=9/14=0.64, P(no)=5/14=0.36 \]

条件概率\(P(a_i|v_j)\)为： \[ P(Wind=strong|yes)=3/9=0.33 \\ P(Wind=strong|no)=3/5=0.60 \\ ... \]

故最终的预测结果为no。

贝叶斯信念网络

贝叶斯最优分类器应用起来代价太大，朴素贝叶斯分类器虽然使用条件独立假设降低了代价，但是很多情况下条件独立假设都难以满足。因此，贝叶斯信念网络做了一个折衷，允许对属性集合的子集应用条件独立假设。

贝叶斯信念网络是一种概率图模型，通过有向无环图（DAG）来表示一系列变量及它们的条件依赖关系和变量集合的联合概率分布。通常用结点表示变量，可以是观测变量、隐藏变量、未知参数和假设等等；用边表示结点间的依赖关系；条件概率表的每个元素对应图中唯一的结点，存储该结点对于其所有直接前驱结点的联合条件概率。

贝叶斯信念网络一条非常重要的性质是：每个结点在其直接前驱结点的值给定后，该结点条件独立于其所有非直接前驱结点。条件独立的定义是：在给定Z的条件下X的概率分布与Y的取值无关，即： \[ \forall x_i,y_j,z_k\ P(X=x_i|Y=y_j,Z=z_k)=P(X=x_i|Z=z_k) \]

条件独立的定义可以扩展到多个变量的情形：即在给定变量\(Z_1,...,Z_n\)的条件下，变量集合\(X_1,...,X_l\)的概率分布与变量集合\(Y_1,...,Y_m\)的取值无关： \[ P(X_1,...,X_l|Y_1,...,Y_m,Z_1,...,Z_n)=P(X_1,...,X_l|Z_1,...,Z_n) \]

朴素贝叶斯分类器即使用了条件独立假设使得\(P(X,Y|Z)=P(X|Y,Z)P(Y|Z)=P(X|Z)P(Y|Z)\)。

贝叶斯网络也可以看作是表示变量之间因果性的因果图，可以进行原因推理或结果预测。例如，假设草坪是湿的记作变量W，那么有多大概率是因为下雨（记作变量R）造成的？那么可以利用贝叶斯网络进行原因推理： \[ P(R|W)=\frac{P(W|R)P(R)}{P(W)}=\frac{P(W|R)P(R)}{P(W|R)P(R)+P(W|\sim R)P(\sim R)} \]

随着贝叶斯网络的结点与边的增加，可以进行更加复杂的因果推断。

总结

贝叶斯学习为基于先验知识的概率学习方法提供了理论基础，在先验知识的基础上，根据观测数据修正先验知识，计算出每个假设的后验概率进而进行预测。可以选择出在给定观测数据下的最有可能的假设即MAP假设，贝叶斯最优分类器通过后验概率的加权结合了所有可能假设的预测结果去得到新实例的最有可能的预测结果。朴素贝叶斯分类器通过条件独立假设增强了其实用性，在很多实际应用中表现很好。贝叶斯信念网络提供了一种条件独立的变量之间更强大的表示方法，使得其可以有更加广泛的应用场景。