为了避免BST退化为单链表,出现了AVL树,但终究是二叉树,难堪大用。
B-Trees
B-Trees可以认为是一种泛化的BST,BST的每个结点只存储单个key,因此最好情况下只能将key space划分为两半,查询复杂度\(O(log_2n)\),为了进一步提高查询的效率,可以令每个结点存储任意数量的排好序的key,即所谓的多路查找树,每个结点的k个key可以将key space划分为k+1段,每个子树负责一段。
m阶B-Tree有着如下性质:
- 每个节点最多有\(m\)个孩子, \(m-1\)个key
- 除根节点外, 所有结点最少有\(\lceil \frac{m}{2} \rceil\)个孩子
- 所有叶子结点都处在同样的深度,即绝对平衡
4阶B-Tree又叫2-3-4树,因为每个结点可以存储1-3个key,即可以有2-4个分叉,因此得名。
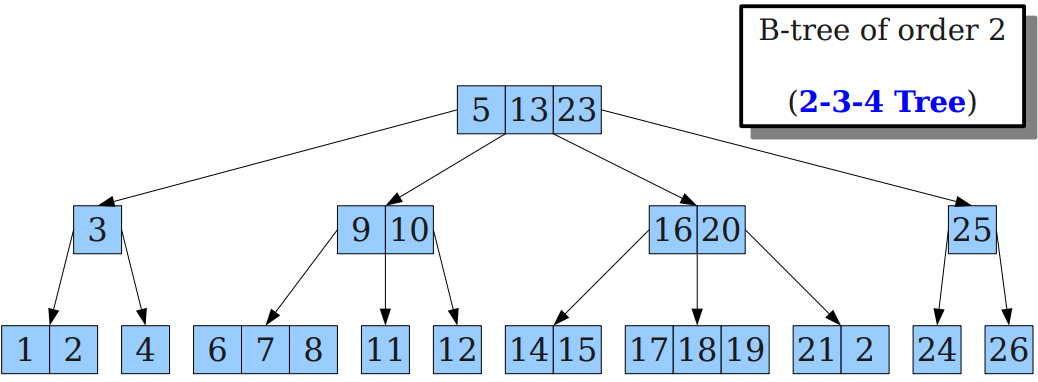
B-Tree的多key存储虽然会减小查询代价,但会导致插入和删除的代价增加,那么人们为啥还要用呢?本质上还是因为磁盘的访问太过耗时,访问磁盘数据的时间由3部分组成:
- 磁头移动到相应的磁道所耗费的时间,大概10ms左右;
- 磁头旋转到相应的扇区所耗费的时间,大概4-5ms左右;
- 在扇区读写数据所耗费的时间,基本可以忽略。
因此,任意一块扇区的访问(读或写)大致需要15ms,数据一般被排列为相邻扇区组成的磁盘块,B-Tree可以极大地减少访问次数,尽管使得磁盘块内的读写代价增加,但这些代价相比于磁盘访问耗时可以忽略不计。
可以通过一个例子感受下B-Tree和BST的差距:假设数据库有\(n=10^6\)条记录,每条记录包含4B的key(如id等)和50B的信息,扇区大小512B,指针大小4B。
- 如果选择BST来存储,每个结点共有62B(key+value+2*pointer),每个扇区可以存储8个记录,由于访问次序是随机的,因此不太可能接连访问同一个扇区内的记录(该情况磁头无需大规模移动,即访问2个记录的时间和访问1个记录相同),故访问每条记录均需要15ms,在\(n=10^6\)条记录中查找任意一条记录最好情况下需要\(log_2n=20\)次查询,共耗时0.3s左右。
- 如果选择4阶B-Tree来存储,每个结点共有414B(最多7个key+7个数据域+8个孩子指针+1个整数记录当前结点的key数目),在\(n=10^6\)条记录中查找任意一条记录需要\(log_4n=10\)次结点查询(0.15s)以及在该结点内部查找对应记录的时间(可忽略),性能大大提升。
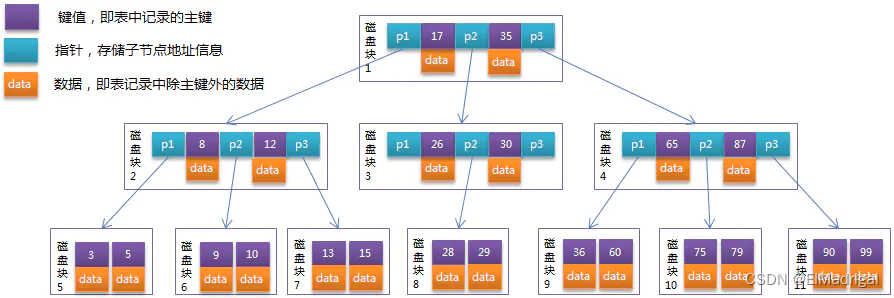
B+ Trees
B+ Tree的非叶结点只存储key,叶子结点存储(key, value)并且将所有叶子链成单链表。
MySQL数据库支持多种存储引擎,不同的存储引擎可能采用不同的索引结构。InnoDB
B+树相比B树的优势有两方面:
- 由于内部结点只保存key,因此内部结点可以存储更多指针,降低树的高度,减少磁盘I/O次数;
- 叶子结点之间通过指针链接,方便区间查询。
红黑树等二叉树相比于B+树要高得多,因此磁盘I/O更加频繁,更适合在内存中查找。
红黑树
是具有如下性质的BST:
- 每个结点要么红要么黑;
- 根结点是黑;
- 红色结点的孩子必须是黑色;
- 所有从根到null的路径均含有相同数目的黑色结点。
跳表
LC 1206
https://oi-wiki.org/ds/skiplist/
Reference
B Trees and B+
Trees. How they are useful in Databases
Balanced
Trees
B-Trees
B+
Review
为什么Mongodb索引用B树,而Mysql用B+树
MySQL索引背后的数据结构及算法原理
Mysql索引BTree、B+Tree详细分解

